Уравнение Капицы

Пусть имеется сеть размера М, т.е. ИС, содержащая М клаттеров. И допустим, что за цикл новый клаттер собрать не удается. Т.е. рассмотрим сначала первый этап роста сети. На копирование одного клаттера требуется М носителей, и всего за цикл их будет скопировано М². Если N — численность популяции, то: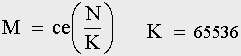

                                                       (31)

Здесь ce(X) ближайшее целое, меньшее или равное числу X. Прирост численности популяции за цикл равен: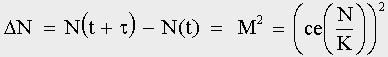

                    (32)

К этому разностному уравнению необходимо добавить  условие завершение цикла. Как только в процессе итераций N(t) достигнет значения, достаточного для сборки нового клаттера, нужно сделать подстановку: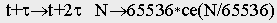

                                                (33)

Вот решение этого уравнения в системе MathCAD (здесь τ = 1, время измеряется в циклах):

Зависимость численности популяции от времени получается такой же, как в модели роста клаттеров по циклам U2(C). Если число собранных за цикл клаттеров  значительно меньше размера сети (второй этап ее роста), то и в этом случае данное разностное уравнение служит хорошим приближением алгоритму. При этом N(t) мало меняется за время τ. Если, к тому же N(t) >> K, то дифференциальное уравнение может служить хорошим приближением разностному.

Здесь τ – время цикла сети, равное постоянной времени Капицы. Этим же уравнением описывается  «теоретическая гипербола».

Важно понимать следующее: зависимость N(t), задаваемая алгоритмом роста сети, может быть описана уравнением Капицы на всем протяжении этого роста. Тем не менее гиперболы роста на этапах до момента начала неолита и после момента начала неолита — отличаются. Дело в том, что рост сети на первом этапе описывается уравнением Капицы лишь приблизительно.
 

Тогда как на втором этапе, когда рост, согласно алгоритму, резко ускоряется, он может быть в точности описан теоретической гиперболой, которая, как мы уже отмечали ранее, является «точечной функцией» (т.е. ее областью определения и ее множеством значений являются 256 фиксированных значений времени и численности), все точки которой лежат на гиперболе, являющейся решением уравнения Капицы.

Поэтому аппроксимирующие зависимости численности от времени до и после начала неолита отличаются, и общее решение «сшивается» из двух различных кривых. И поэтому в момент начала неолита скорость роста как функция времени (теоретически) претерпевает разрыв.

Парадоксальная гиперболическая зависимость численности населения Земли от времени возникает по причине постоянства времени цикла растущей сети.