Сингулярность Дьяконова-Капицы
«Мы свидетели гибели системы мира,
такой, какой мы ее знаем, и находимся
в самом начале формирования новой,
очертания
которой до сих пор неясны».
И. Валлерстайн
- Введение
- Сингулярность Дьяконова-Капицы как момент завершения первого цикла демографического перехода
- Восемь шагов к сингулярности Дьяконова-Капицы
- Зависел ли исторический прогресс на протяжении одиннадцати тысяч лет только от численности населения Земли?
- Существует ли главный исторический цикл?
- Волны Кондратьева на Солнце?
- Какова точность границ исторических периодов?
- Какое событие произошло в 1978 году?
- Существует ли теоретическая формула зависимости численности населения Земли от времени?
- Что же такое сингулярность Дьяконова-Капицы?
- Что за сингулярностью?
- Финализм и 25 сценариев конца света
На существование сокращающихся по закону прогрессии периодов исторического развития впервые указывает историк И.М. Дьяконов в своей книге «Пути истории», [8]:
«Нет сомнения, что исторический процесс являет признаки закономерного экспоненциального ускорения. От появления Homo sapiens до конца I фазы прошло не менее 30 тысяч лет, II фаза длилась около 7 тысяч лет, III фаза – около 2 тысяч лет, IV фаза – около 1,5 тыс., V фаза около тысячи лет, VI – около 300, VII фаза – немногим более 100 лет, продолжительность VIII фазы пока определить невозможно. Нанесенные на график, эти фазы складываются в экспоненциальное развитие, которое предполагает в конце концов переход к вертикальной линии или вернее, к точке так называемой сингулярности. По экспоненциальному же графику развиваются научно – технические достижения человечества, а также, как упомянуто, численность населения Земли».
Термин «сингулярность Дьяконова» впервые появляется в работах А.Д.
Панова. В
аннотации и предисловии к книге Панова «Универсальная эволюция и
проблема поиска
внеземного разума (SETI)», читаем:
«Вводятся представления о масштабно-инвариантном аттракторе планетарной эволюции и его завершении в режиме с обострением "сингулярностью Дьяконова" в первой половине XXI века».
«Удивительной находкой оказалось то, что подход И.М. Дьяконова, который в основу анализа положил последовательность фазовых переходов социальной системы, естественным образом обобщается на всю эволюцию – и биосферы, и цивилизации, начиная с появления жизни на Земле. Эволюция цивилизации в определенном смысле оказывается гладким автомодельным продолжением эволюции биосферы, а точка сингулярности получает статус некоторого переломного или завершающего момента всей четырехмиллиардолетней истории развития жизни на Земле».
Приведенные выдержки воспринимаются с трудом, но даже если не вникать в смысл этой физикалистской абракадабры можно все-таки понять, что Панов определяет сингулярность Дьяконова как предельную точку последовательности дат своих планетарных революций. Такая инициатива представляется выражением самонадеянности, некомпетентности и бестактности ее автора. Здесь важно не только то, что совмещая биосферную и историческую сингулярность, Панов приходит к абсурдным, апокалиптическим результатам. Кризис планетарного цикла А.Д. Панова — отменяется.
Даже и сам термин «сингулярность» Панов понимает неправильно. Действительно, для того чтобы говорить о сингулярной точке истории, эволюции необходимо, чтобы какой-то показатель исторического или эволюционного процесса описывался неограниченно возрастающей за конечный промежуток времени функцией. Поскольку такой показатель в построениях Панова отсутствует, то ни о какой вертикали Снукса-Панова, ни о каком режиме с обострением в первой четверти XXI столетия — не может быть и речи. Так, например, если считать, что ускорение исторического прогресса было не гиперболическим, а экспоненциальным, то «переход к вертикали» занимал бы бесконечно долгое время. И речь в таком случае шла бы не о точке сингулярности, а о некотором конечном (в идеальном случае бесконечном) интервале времени — эпохе перемен.
Говорить об исторической сингулярности или сингулярности Дьяконова стало возможным лишь после работ С.П. Капицы, которым впервые было введено представление о сжатии исторического времени к точке сингулярности эмпирической гиперболы демографического роста. Согласно принципу демографического императива Капицы, именно численность населения Земли в эпоху гиперболического роста и есть та переменная, которая может служить естественной мерой эволюции и развития. Поскольку в формуле Форстера эта переменная в двадцатых годах XXI столетия устремляется к бесконечности, понятие «сингулярность Дьяконова» обретает смысл. В таком случае историческая сингулярность или сингулярность Дьяконова может быть названа сингулярностью Дьяконова—Капицы.
Эта глава написана с единственной целью: противостоять интерпретации понятия «сингулярность Дьяконова» в понимании Панова и дать ему единственно правильное, по мнению автора, определение. Весь представленный нами материал можно разделить на две части. В первой части, сингулярность Дьяконова—Капицы будет определена исходя из развиваемой здесь гипотезы о растущей сети, сопровождающей эволюционный и исторический процесс. Такое определение, разумеется, не может быть бесспорным, поскольку опирается на гипотезу. Так как ошибка здесь недопустима по этическим соображениям, ведь эта историческая сингулярность ассоциируется с именами известного историка и выдающегося популяризатора науки, нами будет еще раз дано ее определение, но уже без всяких ссылок на нашу гипотезу, а на основании лишь известных исторических фактов. Это будет сделано во второй части нашей работы, к которой можно перейти сразу же, не читая первую.
Сингулярность Дьяконова—Капицы как момент завершения первого цикла демографического перехода
Прежде всего, покажем, что сингулярность Дьяконова—Капицы, согласно предлагаемой здесь гипотезе, приходится на 2022 год с погрешностью примерно в два, три года и в полном соответствии с демографическими данными. Запишем формулу теоретической гиперболы:
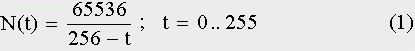
Здесь N(t) — численность в клаттерах (один клаттер содержит 65536 носителей), а t — время в циклах от начала неолита. Моменты времени t = 0, 128, 192, 224, 240, 248, 252, 254, 255 — даты, когда сеть достигает гармонической стадии своего роста. Момент t = 256 — точка сингулярности или время окончания первого цикла демографического перехода, если отсчет времени вести от начала неолита. Если отсчет времени вести от р.х., точку сингулярности получаем прибавлением к дате достижения сетью совершенства, т.е. к 1978 году, времени цикла сети, равного 44-м годам: 1978 + 44 = 2022 г. Постоянная Форстера для теоретической гиперболы равна:
![]()
Если время измерять в годах, а численность в миллиардах человек, то формула (1) приобретает вид:

Но именно так и выглядит эмпирическая гипербола, описывающая рост численности населения Земли за последние сорок с лишним тысяч лет:

Эта гиперболическая зависимость, из семейства гипербол Форстера, лучше всего задает рост численности населения мира от 40.000 г. до н.э. до 1970 г. по данным Мак-Эведи, Джоунса (1978) и Кремера (1993) для периода от 40.000 г. до н.э. до 1950 г. н.э., а также Бюро переписей США за 1950—1970 гг. [13]
Теоретическая гипербола (3), а значит и (1) практически тождественна гиперболе (4), следовательно, 2022 год, действительно, точка сингулярности. На самом деле гипербола (4) описывает с хорошей точностью рост населения мира вплоть до 1978 года. Это вытекает из того простого факта, что теоретическая гипербола, по определению, должна проходить через точку (1978; 655362), что соответствует демографическим данным с погрешностью для времени (1978 г.) максимум в два года:
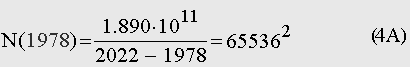
Построим в одних координатных осях гиперболу (4) и график интерполяции данных по численности населения мира с 1960—1990 гг., International Data Base (IDB) с шагом в один год.
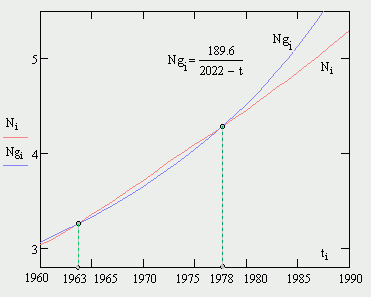
Рис 1С. Гипербола (4) и интерполяция демографических данных за 1960—1990 гг.
Последнее максимальное сближение, а фактически пересечение эмпирической гиперболы (4), с графиком интерполяции демографических данных, произошло в 1978 году, а затем эти кривые разошлись навсегда. Поэтому именно 1978-й год можно с достаточным основанием считать моментом окончания гиперболического роста и началом первого цикла демографического перехода. Следовательно теория полностью соответствует демографическим данным. Причем 1978-й год с точностью до одного, максимум двух лет, и есть тот момент времени, когда сеть достигает совершенства, а 2022-й год (1978 + 44 = 2022) соответственно — конец первого цикла демографического перехода, или точка сингулярности теоретической и эмпирической гипербол демографического роста.
Согласно предлагаемой здесь гипотезе на кривой роста численности населения Земли имеется пять особых точек:
- 1,9 млн. лет назад — старт роста сети человека, начало эволюции Homo sapiens.
- 9 тыс. лет до н.э. — переход ко второму этапу роста сети; начало неолита и взрывного демографического роста.
- 1978 год — сеть достигает совершенства, эволюция человека заканчивается.
- 2022 год — окончание первого цикла демографического перехода; сингулярность Дьяконова—Капицы.
- 2065 год — конец второго цикла демографического перехода,
завершение операции
репликации, старт сети пятого ранга, начало эволюции «post Homo».
Из них, на первый взгляд, самой незначительной представляется точка, соответствующая моменту окончания первого цикла демографического перехода. Этот момент времени: 2022 год, действительно, по значимости, видимо, уступает всем другим эпохальным моментам роста сети человека. Так, достижение сетью совершенства в 1978 году представляется куда более важным событием. Тем не менее оно так и прошло незамеченным. Следовательно, вряд ли следует ожидать каких-то судьбоносных событий, приуроченных и к этой дате. И, конечно же, не будет никаких катастроф. Дело в том, что 2022-й год находится в пределах погрешности, с которой вычисляются времена «ухода на бесконечность» всех эмпирических гипербол демографического роста.
А ведь именно с этой датой связывают разные авторы демографический, технологический и даже биосферный кризис. Если исходить из предлагаемой здесь гипотезы, никаких кризисов и катастроф в ближайшие два десятилетия не произойдет. Значение сингулярности Дьяконова—Капицы, как особого момента эволюции и развития, не в том, что с ней связаны какие-то события планетарного масштаба. Сингулярность Дьяконова—Капицы — сингулярность фиктивная, недостижимая; это всего лишь математическая абстракция, предельная точка, к которой сходятся и до которой никогда не доходят сжимающиеся по закону прогрессии исторические циклы. Такое определение полностью соответствует тому описанию ускоряющегося исторического процесса, которое мы находим в работах И.М. Дьяконова.
Отсчет исторического времени ведется от момента начала неолита, т.е., согласно теории, от момента 9100 лет до н.э. (±250 лет). Знаменатель прогрессии равен 1/2. Длительность первого исторического периода равна половине отрезка времени, отложенного от начала неолита до сингулярности Дьяконова Капицы: (2022 + 9100)/2 = 5560 лет. Каждый последующий период в два раза короче предыдущего, а численность населения Земли на момент его завершения удваивается. Всего периодов восемь, и ход всемирной истории можно рассматривать как последовательность из восьми шагов по оси времени, в которой каждый последующий шаг в два раза короче предыдущего.
Более точный образ дает лестница, у которой каждая следующая ступенька в два раза короче и выше предыдущей. (Время откладывается по горизонтали, размер сети или численность населения Земли — по вертикали.) При этом в качестве инварианта исторического процесса выступает постоянная Форстера: произведение численности населения Земли на момент завершения каждого из восьми исторических периодов на его длительность, есть величина постоянная и равная 232, если время измерять в циклах сети человека, или примерно 200∙109 — если в годах.
Для сингулярности Дьяконова—Капицы можно предложить и несколько иной образ. На шкале исторического времени существуют две «опорные точки» для определения исторических периодов — это момент начала неолита 9100 лет до н.э. и сингулярность Дьяконова—Капицы — 2022 год. Первый исторический цикл отсчитывается от начала неолита до середины отрезка -9100 — +2022 гг., а каждый последующий заключен между концом предыдущего и серединой отрезка, соединяющего этот конец с сингулярностью Дьяконова—Капицы. Сведем все данные в таблицу.
| Номер «гармони-ческого» цикла | 42142 | 42270 | 42334 | 42366 | 42382 | 42390 | 42394 | 42396 | 42397 |
| Время начала цикла (год) | 9100 днэ | 3550 днэ | 760 днэ | 630 | 1325 | 1674 | 1848 | 1934 | 1978 |
| Численность населения
Земли |
224 | 225 | 226 | 227 | 228 | 229 | 230 | 231 | 232 |
| Количество циклов до сингулярности Дьяконова-Капицы | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| Номер исторического периода | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| Длительность периода в
циклах |
128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | |
|
Время начала и время конца исторического периода (теория) |
9100 днэ -- 3550 днэ |
3550 днэ -- 760 днэ |
760 днэ -- 630 нэ |
630 -- 1325 |
1325 -- 1674 |
1674 -- 1848 |
1848 -- 1934 |
1934 -- 1978 |
1978 -- ???? |
| Этап становления ноосферы | Неолит |
Первые цивили- зации |
Фило- софия |
Эти- ка |
Эсте- тика |
Наука |
Тех- ника |
Техно- логия |
|
| Фаза | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| Время начала и время конца исторического периода (Периодизация Дьяконова) |
10000 днэ -- 3000 днэ |
3000 днэ -- 1000 днэ |
1000 днэ -- 540 нэ |
540 -- 1540 |
1540 -- 1840 |
1840 -- 1950 |
1952 -- ???? |
||
| Период | 6 | 7 | 8 | 9 | 10 | 11 | |||
| Время начала и время конца исторического периода (Периодизация Капицы) | 9000
днэ -- 2000 днэ |
2000
днэ -- 500 нэ |
500 -- 1500 |
1500
-- 1840 |
1840 -- 1965 |
1965 -- 2007 |
Таблица 1С. Данные по историческим периодам, сокращающимся по закону прогрессии к точке сингулярности гиперболы Форстера в периодизациях И.М. Дьяконова, С.П. Капицы и теоретической — от неолита до 1978 года.
И.М. Дьяконов различает восемь фаз или ступене́й исторического процесса. Такое разделение соответствует восьми стадиям роста сети человека от начала неолита до наших дней. Отличие теоретической периодизации от периодизации Дьяконова, во-первых, в том, что первая, первобытная фаза исторического процесса у И.М. Дьяконова относится не к началу неолита, а к предшествовавшему ему позднепалеолитическому периоду. И, во-вторых, пятый исторический период, 1325–1674 гг. (согласно теории), в периодизации Дьяконова — отсутствует.
В остальном наблюдается очень хорошее совпадение. Здесь нужно еще учесть то, что данные по периодизации Дьяконова, приведенные в таблице, лишь приблизительно очерчивают границы исторических фаз. Сам И.М. Дьяконов четко эти границы не определял, видимо, по принципиальным соображениям. И это понятно, т.к. критерием исторического изменения в его работах выступает развивающееся человеческое общество (Мир-система), границы фаз условны, а длительность междуфазовых переходов может быть значительной.
Периодизация Капицы, в которой границы исторических периодов определены гораздо более четко, также мало отличается от теоретической. У С.П. Капицы после неолита — шесть исторических периодов, у И.М. Дьяконова — семь фаз исторического процесса, теоретически же имеется восемь периодов роста сети человека. Теоретическая периодизация почти не отличается от экспертных периодизаций как по количеству исторических периодов, так и по их датировке. Если при этом учесть, что И.М. Дьяконов никогда не считал результаты своих исследований бесспорными и окончательными, можно констатировать совпадение, причем с хорошей точностью, теории и экспертных оценок. Но тогда восемь ступеней Дьяконова — это восемь периодов роста сети человека. Еще одна ступень, палеолитическая, первая у И.М. Дьяконова, существует и в теории, но гораздо менее значима, чем последующие.
Согласно предлагаемой здесь гипотезе, главной причиной цикличности исторического процесса, универсальной эволюции (прогрессия эволюции) и экономики (циклы Кондратьева, Кузнеца, Жугляра, Китчина) является циклически растущая иерархическая сеть. Что находится в полном соответствии с тезисом историка Вильяма Грина о том, что в основе исторической периодизации должна лежать некая теория исторического изменения. Здесь в этом качестве выступает теория растущей через гармонические стадии сети человека, она и есть лидирующий сектор или главный источник изменений. Моменты гармонического достижения для сети или моменты междуфазовых переходов для социума по И.М. Дьяконову — это эпохи перемен, когда рождаются новые качественные изменения в природе человека.
Причиной исторических циклов являются качественные изменения в носителе сети, т.е. в человеке. Такие изменения происходили на всем протяжении эволюции человека с момента появления рода Homo, причем всегда носили скачкообразный характер, т.е. появлялись за ничтожное в сравнении с временем эволюции время. Сеть человека прошла 42397 циклов роста с момента своего старта 1,9 млн. лет назад до 1978 года. Возможно, в течение каждого из них носитель претерпевал некоторые изменения, но настоящие скачки приходились на моменты достижения сетью гармонического размера.
Это были генетические изменения, приводящие к росту головного мозга, появлению новых или развитию уже существующих образований в его коре таких, как зоны Брока и Вернике. Но так ли это для исторического времени, которое мы отсчитываем от начала неолита? Если исходить из предлагаемой здесь гипотезы, восемь ступеней исторического развития также были обусловлены прогрессивными изменениями на генетическом уровне носителя сети, т.е. человека. Иначе говоря, мы качественно отличаемся от наших предков, живших всего лишь несколько тысяч лет назад.
Согласно исследованиям ученых из американского Университета штата Юта, мощный рост населения Земли в последние пять тысяч лет, привел к беспрецедентному ускорению эволюции человечества. Современный человек генетически больше отличается от людей, живших 5 тысяч лет назад, чем те же люди от неандертальцев, вымерших более 30 тысяч лет назад.
Это не означает, конечно, что в эпоху перемен все появляющиеся на свет представители рода человеческого обладают некими новыми возможностями. Дело в том, что у авангардной системы эволюции, каковой является род Homo, всегда был свой авангард, на первых порах немногочисленный, но достаточный для прогрессивных изменений, назревших в социуме. Более того, далеко не все ныне живущие представители рода человеческого обладают способностями, соответствующими восьмой ступени исторического развития. На самом деле имеется полный спектр типов личности, с разными способностями и с разным уровнем развития, и состав этого спектра, видимо, не случаен, т.к. обеспечивает сети необходимую динамику ее роста.
На момент начала неолита в обществе древних охотников и собирателей появились сначала немногочисленные представители, способные к значительно более сложной деятельности, без которой невозможен оседлый образом жизни. Для того, чтобы заниматься земледелием и скотоводством, строить прочные жилища, производить и обменивать товары нужен был человек другого типа, с другой нервной организацией, иначе работающим мозгом. И этот человек появился по всей Ойкумене, причем за очень короткий промежуток времени. Такие скачкообразность и синхронистичность изменений характерны и для всех других ступеней исторического развития.
Следующая ступень исторического развития (ее начало 3500 лет до н.э.) связана с появлением первых цивилизаций. Именно тогда появились первые города, древние государства, были воздвигнуты такие грандиозные сооружения, как египетские пирамиды, возникли различные формы политеистической религии, появилась письменность и в зачаточном состоянии наука… Какие изменения происходили с человеком в эту эпоху? Чем коренным образом он отличался от своего предшественника, неолитического человека? Ответ на этот вопрос не так-то прост, и во всей полноте его могут дать лишь специалисты по истории древнего мира.
Последующие ступени отмечены нами как времена возникновения первых философских учений — революция в мировоззрении, становления мировых религиозных течений — революция в этике, возникновение различных форм искусства — революция в эстетике. Далее, идут наука, техника, технология. Конечно, все это лишь идентификаторы этапов становления ноосферы, каждый из которых определяет целый список изменений, произошедших с человеком и обществом. Составить такой список для каждого исторического этапа задача исторической, психологической или какой-нибудь другой, не существующей на данный момент науки о человеке.
Каков же итог? Что же такое сингулярность Дьяконова—Капицы? Это предел, к которому устремляются сжимающиеся по закону прогрессии исторические циклы. Так понимал ее и И.М. Дьяконов. Сингулярность эта чисто математическая, в реальности фиктивная, поэтому никаких катастрофических событий в 2022 году ожидать не следует. Какой же прогноз на ближайшее будущее можно сделать, если исходить из предлагаемой здесь гипотезы? Какие перемены ждут систему «все человечество в целом» за сингулярностью Дьяконова—Капицы?
- Рост населения мира будет идти и после прохождения сингулярности Дьяконова—Капицы.
Когда сеть начнет «нажимать на тормоза» сказать трудно, возможно, в сороковых —
пятидесятых годах нынешнего века. Вопреки всем неблагоприятным прогнозам рост этот
будет сопровождаться также и всемирным экономическим подъемом.
Будет улучшаться качество жизни, расти ее продолжительность как в развитых странах
с неизменной численностью, уже прошедших переход, так и в странах третьего мира,
находящихся в его процессе.
При подходе к 2065 году возможны некоторые катаклизмы по причине гипотетического явления демографической отсечки, которое заключается в следующем: В момент завершения построения второго финального клаттера в 2065 году произойдет старт сети пятого ранга, и все «избыточные носители», появившиеся «по инерции» после 2065 года, впервые за всю историю роста сети человека не смогут быть установлены в сеть и окажутся вне ее. Поскольку феномен сознания, видимо, связан с сетью, будет, вероятно, зафиксирован невиданный рост числа психически больных людей, возможны также какие-то другие негативные явления, например, природные катастрофы или локальные военные конфликты с человеческими потерями, в результате которых будут удалены из социума все «избыточные носители». Но это лишь предположение.
Во всяком случае, не следует ожидать плавного выхода кривой роста «на полку», иначе говоря, постепенного, в течение 100 лет приближения к горизонтальной асимптоте, что обычно прогнозируют в последней фазе демографического перехода. Напротив, в 2065 году будет зафиксирован скачок скорости роста, в процессе которого она очень быстро, по историческим меркам мгновенно, упадет до нуля. Сама же численность населения Земли как функция времени за этот короткий промежуток времени, возможно в колебательном режиме, примет свое предельное значение. - Никакой катастрофы или даже просто какого-то фазового перехода под названием
технологическая сингулярность в XXI столетии, и вообще никогда в будущем, не
случится.
Ничего, ровным счетом ничего качественно нового не будет создано, когда
компьютерные чипы, полученные на пределе возможностей технологий, подчиняющихся
закону Мура, и компьютерные системы на их основе обретут невиданную мощь.
Сознания им все равно не обрести никогда — это прямое следствие нашей гипотезы, и
потому заменить, вытеснить, поработить человека — они так никогда и не смогут.
Роль их всегда будет чисто утилитарной.
Но что ждет в таком случае цивилизацию в будущем? То, что и предсказывают трансгуманисты: дальнейшая эволюция (управляемая, в отличии от биологической, человеком), возникновение в ее процессе нового вида на основе киборгизации, т.е. симбиоза человека и машины, переход в другие темпомиры и на другой «носитель сознания», освоение Солнечной системы, взрывной рост численности через миллион лет и т.д.
- В период 2008–2022 гг. мы станем свидетелями свертывания циклического процесса,
наблюдавшегося последние четыреста лет, под названием «Одиннадцатилетний солнечный
цикл».
Большой солнечный конвейер, открытый Дэвидом Хезевеем и его коллегами, в
обозначенное время будет либо полностью остановлен, либо замедлен до предела, т.к.
считается твердо установленным факт связи скорости потоков плазмы с интенсивностью
появления солнечных пятен.
Медленное движение плазмы приводит к снижению солнечной активности, быстрое — к ее
повышению, причем с запаздыванием примерно в 20 лет. Всплески солнечной активности
будут носить спорадический характер, с тенденцией к спаду, и 24-й солнечный цикл
так и не состоится.
После 2022 года одиннадцатилетняя циклическая активность Солнца прекратится
полностью и навсегда. На смену одиннадцатилетнему придет цикл со средней
продолжительностью 45 (?) минут или несколько иной.
В отличие от 160-ти минутного цикла колебаний яркости Солнца в целом, открытого в 70-х годах прошлого века в КРАО, продолжительность которого является некой космологической константой (160.0101 ± 0.0016 мин.), новый 45-ти минутный цикл, аналог своего предшественника, будет представлять собой, вероятно, локальный феномен переменной длительности (30—60 минут (?); суммарная продолжительность четырех последовательных циклов, составляющих один трехчасовой, есть константа) и проявляться в виде вспышек или каких-либо других «точечных» возмущений на поверхности Солнца. Поначалу они будут очень слабыми, и вопрос о возможности их регистрации в 2022 году остается открытым. Лишь по прошествии тысячелетий, трехчасовой цикл (четыре 45-ти минутных цикла, предположительно, по аналогии, будут составлять основной трехчасовой), в будущем главный цикл всех эволюционных процессов, начнет набирать силу. - Если причины глобального потепления связаны не только с техногенной деятельностью цивилизации, но также с повышенной в ХХ веке солнечной активностью, то после 2022 года глобальное потепление может и закончиться. Более того, вместе с полным завершением одиннадцатилетней солнечной активности может даже начаться эра глобального похолодания, как это уже случалось в истории во времена малого ледникового периода (минимума Маундера).
Сингулярность Дьяконова—Капицы как дата ухода на бесконечность эмпирической гиперболы демографического роста
Здесь мы попытаемся определить сингулярность Дьяконова—Капицы, не опираясь ни на какие гипотезы, а исходя лишь из непреложных фактов истории и демографии. Это не означает, конечно, что основной текст будет полностью свободен от разного рода далеко не бесспорных предположений, но окончательные выводы будут сделаны на независимой от них основе. Алгоритм восьми шагов, применяемый для расчета границ исторических периодов, — всего лишь феноменологическая схема. Почему эта феноменология дает результаты, столь близкие к экспертным оценкам, — непонятно.
Никакого описания периодов или фаз исторического развития здесь приведено не будет, все это есть в книге И.М. Дьяконова «Пути истории». [8] Отметим также, что циклы, которые здесь рассматриваются, — это глобальные исторические циклы, т.е. циклы всей Мир-системы.
Восемь шагов к сингулярности Дьяконова—Капицы
Прежде всего введем две важнейшие для мировой истории даты: первая это момент начала неолита, возьмем (условно конечно, т.к. время начала первого исторического периода определено с некоторой точностью) за эту дату 9100 лет до н.э. Почему неолит? Потому что это начало мировой истории (и это считается общепризнанным), т.е. именно в этот момент времени начинается мировой исторический процесс и процесс взрывного гиперболического роста населения Земли. Вторая дата – это момент Т0, так называемая точка сингулярности закона роста численности населения Земли, когда знаменатель в формуле Форстера, обращается в нуль.
![]()
Здесь С — постоянная Форстера, равная 190*109 лет, а Т0 — 2026 год, когда численность населения Земли становится бесконечной при условии неизменности закона роста. В начале шестидесятых годов, когда Форстер проводил свои исследования, демографический переход еще не начался, и возможность катастрофического перенаселения Земли казалась вполне реальной. Эта дата — 2026 год, определенная с погрешностью в несколько лет, обладает, очевидно, не меньшей значимостью для глобального исторического процесса, чем момент начала неолита.
Почему? Во-первых, потому, что в этот момент времени, очевидно, перестает выполняться закон гиперболического роста, остававшийся неизменным в течение многих тысячелетий. На самом деле отклонение от гиперболического роста было зафиксировано за несколько десятков лет до этого события, но дата Т0, несомненно, играет важную роль, т.к. наряду с постоянной Форстера С полностью определяет эмпирическую гиперболу демографического роста.
И, во-вторых, во второй половине двадцатого века начался глобальный демографический переход, явление, хорошо изученное для отдельных, прошедших переход стран. Переход, истинная причина которого (называются десятки причин) до сих пор остается непонятной и даже загадочной. Несомненно только то, что он является глобальным, т.е. это согласованный для всех стран и народов процесс; происходит он в XXI веке, после него численность населения Земли стабилизируется и расти больше не будет. Несомненно также и то, что глобальный демографический переход явление не только демографическое, но также социальное и историческое.
Итак, существуют две важнейшие даты мировой истории. Момент начала неолитической революции, времени, когда по всей Ойкумене происходит, причем по историческим меркам мгновенно, переход от охоты и собирательства к скотоводству и земледелию. И точка сингулярности эмпирической гиперболы демографического роста, определяющая момент окончания длившегося тысячелетиями гиперболического роста населения Земли и время прохождения демографического перехода. Назовем эту демографическую и историческую сингулярность «сингулярностью Дьяконова—Капицы». Отметим, что обе эти даты — реальные исторические вехи, не связанные ни с какими теориями.
За момент начала неолитического периода берем 9100 год до н.э., а время Т0 положим равным Т0 = 2022 г. Постоянную С в формуле Форстера, примем равной 190∙109 лет. Форстер получил свою постоянную, анализируя данные за последние две тысячи лет. С учетом данных от настоящего времени до неолита, лучше работает формула Хорнера, где С = 200∙10 9 лет, Т0 = 2025 год. Величины С = 190∙109 лет, Т0 = Tsingul = 2022 год, Tneol = -9100 год лежат в пределах погрешности, с которой они известны и выбираются таковыми лишь для достижения полного совпадения с ранее полученными результатами.
Для дальнейшего нам понадобятся некоторые сведения из элементарной математики. Гипербола y = 1/x обладает тем очевидным свойством, что при уменьшении аргумента в два раза, ее значение возрастает в два раза. Геометрическая прогрессия со знаменателем 1/2 обладает одной особенностью, выделяющей ее среди других прогрессий. Она заключается в том, что каждый последующий ее член, будучи отмечен точкой на числовой оси, есть середина отрезка, соединяющего точку, изображающую предыдущий член и точку, представляющую предел прогрессии (точку нуль). Иначе говоря, члены этой прогрессии можно отметить последовательностью шагов по числовой оси, в которой каждый последующий шаг вдвое короче предыдущего. Пусть теперь аргументами гиперболы будут члены геометрической прогрессии, с первым членом равным единице и знаменателем 1/2:
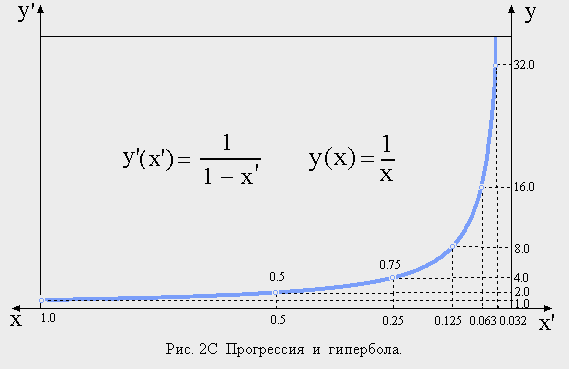
Тогда последовательность значений аргумента будет составлять бесконечно убывающую прогрессию со знаменателем 1/2, а последовательность значений функции, соответственно, — возрастающую прогрессию со знаменателем равным двойке. Произведение x*y будет постоянно и равно единице. Если перейти к системе координат с началом, сдвинутым на единицу в направлении оси Х, а саму эту ось обратить, то уравнение гиперболы примет вид: y'(x') = 1/(1-x'). Последовательность точек на числовой оси, которая в исходной системе определялась бесконечно убывающей прогрессией, в смещенной системе задается последовательностью сумм этой прогрессии.
Применим эту математику для разбиения всей истории развития цивилизации от неолита до наших дней. Формула гиперболы мирового демографического роста имеет вид: Где Т0 = 2022 + 9100 = 11122 год — дата сингулярности, если время отсчитывать от начала неолита. Составим теперь последовательность времен по следующему правилу, которое назовем алгоритмом восьми шагов:
• во-первых, все времена будем отсчитывать от момента начала неолита, и первый член этого ряда будет равен нулю;
• второй член этого ряда и первый из восьми шагов шаг к сингулярности Дьяконова— Капицы — это точка на оси времени, которая делит пополам отрезок времени от неолита до сингулярности Дьяконова—Капицы, т.е. 11122/2 = 5561;
• остальные члены этого ряда определяются последовательностью оставшихся семи шагов по оси времени, в которой каждый следующий шаг вдвое короче предыдущего. Предел этой прогрессии — сингулярность Дьяконова—Капицы.
Вычислим, в соответствии с обозначенным здесь алгоритмом, восемь исторических периодов и пересчитаем их, взяв за начало отсчета привычную дату — нулевой год н.э.:

Рис. 3С. Восемь ступеней исторического развития. Отсчет времени идет от Р.Х.
Таким образом, получаем восемь ступеней, периодов или фаз исторического развития. При этом продолжительность каждого последующего периода в два раза меньше предыдущего, численность населения мира за время его развертывания удваивается, а инвариантом процесса является постоянная Форстера. В качестве показателя исторического изменения при периодизации по алгоритму восьми шагов выступает растущая по гиперболическому закону численность населения Земли.
Казалось бы, в полученных результатах нет ничего особенного — это всего лишь математика. Можно было бы взять любой момент времени в прошлом и 2022-й год, рассчитать таким способом восемь исторических периодов, и численность населения также будет удваиваться от периода к периоду. Но оказывается, что лишь тогда, когда алгоритм стартует с момента начала неолита, разметка исторического времени на периоды соответствует реальности. Следовательно, существуют девять фиксированных, особенных значений параметра «численность населения Земли», при достижении которых и происходят фундаментальные исторические изменения в человеке и обществе.
На вопрос почему это так? — ответа нет. Так же как и на вопрос о том, точные ли даты исторического времени соответствуют таким значениям численности, или алгоритм задает лишь их математические ожидания. Значения этих девяти «квантовых чисел» рассчитываются по очень простому правилу: численность населения Земли на момент начала неолита умножается на двойку в степени от нуля до восьми. Или делится, если подсчет начинать с конца восьмого периода (с 1978 г).
В таблице 2С отмечены периоды или фазы исторического процесса в соответствии с периодизацией И.М. Дьяконова, С.П. Капицы и по алгоритму восьми шагов. Очевидно, имеется очень неплохое соответствие как по количеству исторических периодов, так и по границам, в которых они очерчены.
| Номер исторического периода | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| Численность населения
Земли |
224 | 225 | 226 | 227 | 228 | 229 | 230 | 231 | 232 |
| Количество циклов до сингулярности Дьяконова-Капицы | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|
Время начала и время конца исторического периода (теория) |
9100 днэ -- 3550 днэ |
3550 днэ -- 760 днэ |
760 днэ -- 630 нэ |
630 -- 1325 |
1325 -- 1674 |
1674 -- 1848 |
1848 -- 1934 |
1934 -- 1978 |
1978 -- ???? |
| Фаза | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| Время начала и время конца исторического периода (Периодизация Дьяконова) |
10000 днэ -- 3000 днэ |
3000 днэ -- 1000 днэ |
1000 днэ -- 540 нэ |
540 -- 1540 |
1540 -- 1840 |
1840 -- 1950 |
1952 -- ???? |
||
| Период | 6 | 7 | 8 | 9 | 10 | 11 | |||
| Время начала и время конца исторического периода (Периодизация Капицы) | 9000
днэ -- 2000 днэ |
2000
днэ -- 500 нэ |
500 -- 1500 |
1500
-- 1840 |
1840 -- 1965 |
1965 -- 2007 |
2007 -- ???? |
Таблица 2С. Исторические периоды. Данные по алгоритму восьми шагов, а также периодизации И.М. Дьяконова и С.П. Капицы.
И не играет большой роли то, что у И.М. Дьяконова семь фаз после неолита, а у С.П. Капицы — только шесть. И не суть важно, что нет точного совпадения их границ. Ведь это экспертные, а значит, субъективные оценки, а потому тем более удивительными выглядят имеющиеся совпадения. Первую фазу периодизации Дьяконова, палеолитическую, можно было бы включить и в периодизацию по обозначенному здесь алгоритму. Хотя по значению она стоит все-таки ниже, чем фазы после неолита.
Последнюю восьмую фазу, посткапиталистическую, при том, что длительность ее не определена, И.М. Дьяконов связывает с наличием трех диагностических признаков ее начала. Это, во-первых, новые степени свободы для человека: плюрализм не только мнений, но и религий, во-вторых, уровень развития науки, достигший такой высоты, что военные технологии способны запросто уничтожить жизнь на Земле, и, в-третьих, — революция в электронике и информатике, вытеснение книги компьютером и телевизором. Ее начало, 1952–1953 гг., И.М. Дьяконов определяет временем испытаний ядерного оружия в США и СССР. Понятно, что такое определение достаточно условно.
Если, например, считать восьмой фазой теоретический период 1934—1978 гг., то в таком качестве он также смотрится очень не плохо. Во-первых, этот период хорошо соответствует четвертому Кондратьевскому циклу (циклы Кондратьева являются в равной мере и историческими циклами), который ограничен 1929–1981 гг., и начало фазы — это время экономического подъема. И, во-вторых, все признаки, обозначенные И.М. Дьяконовым в начале периода 1934–1978 гг. здесь уже присутствуют, правда, пока только в форме новаций, т.е. в умах изобретателей и ученых. Действительно, в 1936 году А. Тьюрингом были заложены теоретические основы вычислительной техники, а фундаментальные достижения недавно возникшей ядерной физики послужили основой для всех последующих технологических инноваций в этой области. Что же касается телевидения, то оно существовало тогда уже в реальности.
Конец восьмой фазы, 1978 год, — это время, когда была создана концепция персонального компьютера как индивидуального помощника, усилителя интеллекта, офисной машины, проводника в мир виртуальной реальности. Тогда же возникли сетевые технологии и, в частности, Интернет, была создана концепция постиндустриального информационного общества. В таком представлении посткапиталистическая фаза начинается в 1978 году, когда цикличности исторического процесса приходит конец, и длительность ее не определена.
Еще одно, и последнее отличие теоретической периодизации в том, что она включает еще один исторический период 1325—1674 гг. Существовал ли он в реальности — судить историкам. Но не будем далее анализировать причины различий, ведь периодизация И.М. Дьяконова не догма, что прекрасно понимал и отмечал и сам ее автор. Совпадение результатов феноменологической теории, построенной на основе простого алгоритма и независимых экспертных оценок, представляется здесь гораздо более важным.
Что же еще заставляет верить в предложенную здесь простую схему построения исторических периодов?
Во-первых, то, что последний исторический период 1934–1978 гг. очень хорошо вписывается в четвертый экономический цикл Кондратьева: 1929–1981 гг. А предпоследний, 1848–1934 гг., — прекрасно соответствует объединению второго и третьего цикла Кондратьева: 1844–1933 гг. Экономические циклы Кондратьева, как отмечал известный историк Фернан Бродель, являются в равной мере и историческими.
Во-вторых, численность населения Земли удваивалась в течение каждого из восьми исторических периодов и в конце последнего, 1934–1978 гг., увеличилась, по сравнению с моментом начала неолита, в 256 раз. Сам по себе этот факт не вызывает удивления — это просто элементарная математика. Странно другое. Эта величина достигла в 1978 году весьма круглого значения — 4,3 млрд. человек, а это 232. В 1934 году, как и предсказывает алгоритм, эта численность составляла 2,16 млрд., т.е. была в два раза меньшей. Является ли такое совпадение случайным, или за ним кроется нечто большее?
На момент начала неолита, согласно алгоритму восьми шагов, а также в полном соответствии со значением, которое дает эмпирическая гипербола, на Земле проживало 4,3*109/256 = 224 человек. Но в таком случае, возможно, до неолита также существовало восемь (или семь) исторических эпох (или периодов эволюции человека), таких, что численность человечества по истечению каждого из них также удваивалась. Неолит при этом оказывается посередине 15 исторических периодов. На такую же симметрию в своей периодизации указывает и С.П. Капица.
В момент начала эволюции численность первых представителей рода Homo составляла 217, что соответствует данным палеоантропологии, согласно которым она была порядка 100000. Возможно, конечно, — все это просто игра с числами, однако число 2 играет ключевую роль в схеме прогрессия—гипербола (Рис. 2С). А эта схема, похоже, имеет прямое отношение к реальности.
В-третьих, применяемый здесь алгоритм построения исторических периодов имеет связь с работами по теоретической демографии С.П. Капицы. Действительно, длительность первого цикла демографического перехода в его феноменологической теории (1965– 2007 гг.) примерно равна продолжительности последнего периода по алгоритму восьми шагов 1934—1978 гг. Историческое время у него также сжимается по закону прогрессии, причем показатель этого сжатия лежит в пределах от двух до трех.
В-четвертых, показатель сжатия исторического времени, равный двойке по алгоритму восьми шагов, очень хорошо соответствует среднему коэффициенту ускорения развития мировых цивилизаций, согласно определению этой величины Ю.В. Яковцом. Этот коэффициент у него равен отношению времени существования предыдущей цивилизации к времени существования последующей, и среднее его значения за семь исторических эпох равно 1,8. Причем периодизация Ю.В. Яковца также мало отличается от периодизации по алгоритму восьми шагов как по длительности существования мировых цивилизаций, так и по хронологии их возникновения:
| Мировые цивилизации | Начало | Конец | Длительность, века | Коэффициент ускорения |
| Неолитическая | Х тыс. до н.э. | V тыс. до н.э. | 55-65 | |
| Раннеклассовая | IV тыс. до н.э. | 2я пол. II тыс.до н.э. | 29-33 | 1,9 |
| Античная | XII в. до н.э. | сер.V в. н.э. | 16,5 | 1,9 |
| Средневековая | сер. V в. | сер. XVI в. | 9 | 1,8 |
| Прединдустриальная | сер.XIV в. | 1730 г. | 3, 8 | 2,4 |
| Индустриальная | 1731 г. | 1972 г. | 2,4 | 1,5 |
| Постиндустриальная | 1973 г. | 2130 г. | 1,6 | 1,5 |
Таблица 2D. Хронология и длительность мировых цивилизаций. Ю.В. Яковец, История цивилизаций. М., 1997.
Одним из главных достижений феноменологической теории С.П. Капицы является принцип демографического императива. Этот принцип может быть обобщен и на исторический процесс. В чем суть принципа Капицы? В том, что он провозглашает независимость скорости роста численности населения Земли от всех факторов (прежде всего, различных ресурсов), кроме, собственно, самой этой численности.
В обобщенном варианте принцип Капицы выглядит очень странно, поскольку постулируется причинно-следственная связь между численностью населения Земли и показателями глобального развития. В соответствии с ним получается, что человечество, причем во все времена, развивалось как единая, связная система и развитие это зависело только от численности населения Земли. Здесь важно подчеркнуть, что закон гиперболического роста и принцип демографического императива справедливы только для всего человечества в целом.
Численность населения мира в конце каждого из восьми исторических периодов удваивалась по сравнение с его началом. Поскольку каждый такой период есть не что иное, как ступень на пути исторического развития, разумно предположить, что исторический прогресс, во всем диапазоне исторического времени от начала неолита и до конца двадцатого, века был предопределен и не зависел ни от каких ресурсов. Этот вывод ненамного более странен, чем демографический императив С.П. Капицы.
Под историческим прогрессом здесь понимается сумма всех прогрессивных изменений в человеке и обществе. Таких, например, как создание и совершенствование технологий жизнесбережения, формирование новых учений, возникновение новых мировоззрений, переход к новым, более прогрессивным общественно-экономическим формациям, совершенствование духовного мира человека, научные достижения в различных областях, экономический и научно-технический прогресс.
Существует один показатель прогресса, который можно измерить количественно. Этот показатель — энергия, главный ресурс человечества. Вот что пишет по этому поводу С.П. Капица в своей книге «Сколько людей жило, живет и будет жить на земле»:
«Энергопотребление определяет все возможности развития
общества: обеспечение пищей, уровень промышленного производства,
транспорт, возможности строительства и решения экологических проблем.
Как критерий развития энергия замечательна тем, что может быть измерена
и выражена числом. В этом смысле энергия подобна численности населения,
как объективный критерий роста».
«Подробное исследование связи роста населения мира и глобального
потребления энергии было предпринято Холдpеном.. Обработка его данных
приводит к оценке, показывающей, что суммарное потребление энергии Е~N2
за весь рассматриваемый период».
«Таким образом, до демографического перехода, а практически до 1980 г., рост может быть описан квадратичным гиперболическим законом. Это означает, что сама скорость роста оказывается пропорциональной производству энергии, и на протяжении последних 140 лет, с 1850 до 1990 г., мировое производство энергии выросло в 17 раз, а население — в 4,3 раза. Таким образом, энергетика прямо отвечает скорости роста, как если бы человечество было машиной».
Главный же вывод состоит в том, что за последние 140 лет энергия, потребляемая цивилизацией, росла синхронно с численностью населения Земли. Все это справедливо, разумеется, только в эпоху гиперболического роста. Уже сейчас, в начале демографического перехода, темпы роста производства и потребления энергии начали замедляться, что характерно для постиндустриального общества. Что будет после перехода — покажет только время.
Алгоритм восьми шагов применим только ко всей Мир-системе, т.е. для цивилизации в целом. До неолита исторические периоды (периоды эволюции) представляли собой эпохи, когда изменялся и, прежде всего, генетически лидер биологической эволюции — Homo sapiens. После неолита такие изменения происходят уже с человеческим обществом. Но причина остается, видимо, все той же — изменение носителя цивилизации, человека. В таком случае восемь фаз исторического процесса — это одновременно и восемь ступеней развития человека.
Моменты начала и окончания исторических периодов, междуфазовые переходы, — это девять особых точек на оси исторического времени от неолита до 1978 года. Эти даты и времена, к ним примыкающие есть, по сути, эпохи перемен, когда с человеком и обществом происходили, причем за короткое по историческим меркам время, некие качественные изменения. Эти изменения всегда носили только прогрессивный характер и сохранялись в памяти социума на все последующие времена.
Исторический прогресс, каким бы показателем его ни измерять, протекает, во-первых, циклически (инновационные циклы), во- вторых, скачками. Скачок совпадает по времени с началом следующего исторического периода. Самый ярко выраженный скачок — момент начала неолита. В соответствии с принципом демографического императива Капицы, рост прогрессивных изменений в социуме зависел во все времена только от численности населения Земли (причем зависимость эта всегда носила причинно-следственный характер), а кривая прогресса представляла собой циклическую, возрастающую функцию.
Если же принцип Капицы как причинный закон ошибочен (для сомнений есть веские основания), то связь между численностью и показателями глобального развития следует считать функциональной, сопутствующей связью. Истинная причина роста и развития (причинный закон роста) в таком случае так и остается неизвестной.
Существует ли главный исторический цикл?
В связи с поднятыми проблемами возникает еще один интересный вопрос. Это вопрос о существовании главного исторического цикла и фундаментального отрезка исторического времени. Следует сразу же отметить, что независимо от ответа на него все полученные здесь результаты остаются в силе.
Если последний исторический период 1934—1978 гг. считать еще и последним, т.е. 255-м историческим циклом в череде 254-х циклов, ему предшествовавших, то алгоритм восьми шагов приобретает еще большую простоту и ясность. Действительно, на момент начала неолита до сингулярности Дьяконова—Капицы оставалось 256 циклов и восемь шагов. В ходе продвижения по пути исторического развития этот отрезок времени восемь раз делится пополам. И вот наступает 1978 год, когда до сингулярности остается всего один шаг. Дальнейшее сжатие исторического времени становится невозможным, и алгоритм, исправно служивший в течение одиннадцати тысячелетий, завершает свою работу.
Следует, однако, заметить, что такой подход в детерминистической модели предполагает существование некоего артефакта. Дело в том, что поскольку время начала и конца каждого цикла определяется с полной однозначностью, то историческое время перестает быть однородным. Его однородность теряется не в переносном смысле слова как изменение числа исторических событий в единицу времени, а как предопределенная и инвариантная к потоку исторических событий разметка исторического времени на циклы. Все это указывает на существование циклического процесса непонятной природы.
Что же все-таки заставляет верить в существование кванта исторического времени? Прежде всего, экономические циклы Кондратьева, которые, собственно, и есть, наблюдаемые через призму экономической конъюнктуры периодические циклы, задающие основной ритм мирового экономического и исторического процесса. Периодичность не означает здесь повторяемости, замкнутости по основным показателям, а лишь неизменность интервала времени между моментами начала активации и конца стагнации мирового экономического процесса.
Именно поэтому Кондратьевские циклы называют еще волнами. Длительность их составляет примерно 50 лет (40–60 лет) и постоянство ее на протяжении двух столетий, в условиях меняющейся экономики западных стран, не имеет никакого рационального объяснения. Т.к. границы циклов определяются лишь с некоторой точностью, т.е. размыты и могут перекрываться, то средняя продолжительность Кондратьевского цикла может быть и несколько меньшей 50-ти лет.
Согласно взглядам американского историка, социолога и мыслителя, основателя Мир- системного анализа Иммануила Валлерстайна, именно Кондратьевский цикл является главным циклом Мир-экономик капиталистических стран, определяющим циклическую динамику их развития. Экономические циклы Кондратьева являются также историческими, общецивилизационными циклами и отмечены не только в прошлом и позапрошлом веках. Американские исследователи Дж. Модельски и У. Томпсон насчитывают около двадцати больших циклов развития мировой цивилизации: 930-990-1060-1120-1190-1250-1300-1350-1430-1494-1540-1580–1640-1688-1740-1792-1850-1914-1973-2026 гг.
А инновационные волны в технике и организации производства могут быть прослежены и раньше: в неолите и даже в палеолите. Старт текущего цикла, который будет длиться предположительно до конца первой, начала второй четверти XXI века, Модельски и Томпсон связывают с мировым энергетическим и структурным кризисом 1973–1975 годов. Начало его понижательной волны, которое ожидалось на рубеже тысячелетий, было зафиксировано с опозданием на десять лет в 2008 году. Более тысячи ученых различных стран мира выдвинули в прошлом веке множество версий, объясняющих природу Кондратьевских циклов. Причем разногласия по их датировкам в зависимости от использованных критериев достигают 10–15 лет, т.е. четверти времени продолжительности цикла.
Циклы Кондратьева задают ритм, тактовую частоту мирового исторического процесса, но квантом исторического времени их можно считать лишь с известной натяжкой. Существуют циклы Кузнеца, Жугляра и Китчена, длительность которых равна некоторой части цикла Кондратьева. Выдающийся австро-американский ученый Йозеф Алоиз Шумпетер считал Кондратьевский цикл основным экономическим циклом. В соответствии с его теорией, причиной цикличности является инновационная деятельность, и циклов существует бесконечное множество. Причем цикличность эта носит вложенный характер, т.е. продолжительность каждого более длинного цикла кратна продолжительности более короткого.
Почему же тогда именно Кондратьевский цикл, а не какой-то иной, из более коротких, определяет фундаментальный отрезок исторического времени? Во-первых, потому, что он максимален по длительности в бесконечном ряду инновационных циклов, а сама эта длительность величина менее вариативная, чем длительность коротких циклов. И, во-вторых, потому, что он совпадает с последним историческим периодом, а никакой другой из инновационных циклов таким свойством не обладает.
Т.е. цикл с длительностью равной, скажем, половине Кондратьевского — цикл Кузнеца, согласно алгоритму восьми шагов, ни с каким историческим периодом уже не совпадает. Все это указывает на его выделенное, образующее положение по отношению к другим экономическим и историческим циклам, которые выступают лишь как его производные. Средняя длительность инновационных циклов, так же как продолжительность исторических периодов, получается умножением длительности Кондратьевского цикла на 2N — двойку в некоторой степени, где N целое число N = 0, ± 1,± 2...
Еще одним аргументом, свидетельствующим в подтверждение существования фундаментального отрезка исторического времени, служат работы по теоретической демографии С.П. Капицы. В своих исследованиях он вводит постоянную времени τ (время человека), величина которой (45 лет) примерно равна длительности Кондратьевского цикла. И хотя этот промежуток времени С.П. Капица не связывает ни с каким историческим циклом, демографический переход, согласно его теории, состоит из двух циклов. Их длительность близка к периоду Кондратьевских волн, хотя они и не совпадают по фазе.
Постоянная времени Капицы есть результат анализа различных вариантов роста численности населения Земли в процессе демографического перехода, и была получена только на основании критериев непрерывности и согласованности данных. Этот интервал времени, неизменный на протяжении всего исторического процесса, определяется, по его мнению, внутренней предельной способностью системы человечества и человека к развитию. Такое определение созвучно понятию фундаментального отрезка исторического времени как характерного масштаба длительности исторических изменений.
Еще один довод, возможно, не слишком серьезный, свидетельствующий в пользу существования главного исторического цикла, связан с циклической активностью Солнца.
В середине позапрошлого века было установлено, что количество пятен на Солнце меняется с периодом в 11 лет. В дальнейшем выяснилось, что такие же изменения претерпевают все характеристики хромосферных образований и все виды активного излучения: радиоизлучения, корпускулярного и ультрафиолетового. Т.е. в 11-летнем цикле изменяется состояние всех доступных наблюдению слоев Солнца.
В 1913 году Хэйлом было доказано, что при переходе от каждого 11-летнего цикла к следующему, полярность ведущих групп пятен в обоих полушариях Солнца меняет свой знак. Так что для замыкания по этой характеристике, солнечный цикл должен включать два одиннадцатилетних, т.е. его продолжительность должна составлять 22 года. Этот цикл называют Хэйловским или магнитным.
В начале XXI века американскими учеными был обнаружен так называемый «Большой солнечный конвейер», который представляет собой два потока раскаленной плазмы: южную и северную ветви конвейера. В каждой ветви меридиональный поток у поверхности идет от экватора к полюсу, а встречный противоток — от полюса к экватору. Полный оборот в каждом из них совершается в среднем за 40 лет. Исследователи NASA полагают, что движение этого потока и определяет циклы солнечных пятен.
Возможно, что существует солнечный цикл, аналогичный Кондратьевскому, причем как одиннадцатилетний цикл, так и Хейловский являются лишь его производными. По одиннадцатилетним циклам имеются данные за последние 300 лет. Если сгруппировать эти циклы по четыре, то всего имеется четыре варианта выбора фазы цикла с учетверенной длительностью. Оказывается, что наиболее стабильной или наименее вариативной (минимум дисперсии) является объединенная четверка, синфазная Кондратьевскому циклу. Но статистической значимостью по причине небольшого объема выборки этот факт не обладает. Если обработать данные по методу наименьших квадратов (варьировались продолжительность объединенного цикла и его фаза), то для средней продолжительности солнечного цикла, аналога Кондратьевского, получаем 44.4 года, а конец 24-го цикла приходится на 1977.2 г. Полученные результаты полностью соответствуют данным по циклам Кондратьева и алгоритму восьми шагов.
|
Циклы
|
Номер цикла | 1 | 2 | 3 | 4 | 5 | ||||
| Начало цикла | 1779- ???? |
1844- 1851 |
1891- 1896 |
1929- 1933 |
1973- 1975 |
|||||
| Конец цикла | 1841- 1843 |
1890- 1896 |
1929- 1933 |
1973- 1975 |
???? | |||||
|
Объединенные
четверки солнечных циклов (дата начала) |
Номера 11 летних циклов в четверке |
1-4 | 5-8 | 9-10 | 13-14 | 17-20 | 21-24 | |||
| 1619.0 | 1666.0 | 1712.0 | 1755.2 | 1798.3 | 1843.5 | 1889.6 | 1933.8 | 1976.5 | ||
| Историч. циклы (по алг. 8 шагов) Tsing = 2021.6 Tneol = -9340 (дата начала) |
1622.2 | 1666.5 | 1710.9 | 1755.3 | 1799.7 | 1844.1 | 1888.5 | 1932.8 | 1977.2 | |
Таблица 3С. Солнечные циклы, сгруппированные по четыре. Представлены также данные за 17 век, не обладающие высокой степенью надежности. Расчетные данные для этих объединенных солнечных циклов совпадают с границами исторических циклов при Tsing = 2021.6 г., и Tneol = -9340 г.
Нужно также отметить один поразительный факт, еще более углубляющий аналогию между земными и солнечными процессами. Оказывается, солнечная активность обладает не только свойством цикличности, синхронной с глобальным историческим процессом. Как показали исследования последних лет, связанные с изучением причин глобального потепления, сама эта активность непрерывно возрастала последние несколько сотен, а то и тысяч лет. Возрастала так же, как росла численность населения Земли с момента начала неолита.
Ученые из Института астрономии в Цюрихе во главе с доктором Сами Соланки проверили содержание в гренландском льду особого изотопа бериллия, который образуется под воздействием космических лучей. Исследовались пробы льда из Гренландии так называемые керны, добываемые путем глубокого бурения. Исследования показали, что активность Солнца постоянно росла за последние тысячи лет. Чтобы объяснить это явление, было выдвинуто предположение о существовании некоего суперцикла солнечной активности, на период увеличения размаха которого и приходится наше время.
На втором этапе этой работы, результаты которого были опубликованы в журнале «Nature», ученые работали уже не с пробами льда, а с остатками древних деревьев и со следами изотопа углерода, который образуется в атмосфере под влиянием космических лучей. Данные «по углероду» продолжили данные «по бериллию», и ученым удалось построить график солнечной активности за последние одиннадцать тысяч лет, т.е. до конца последнего оледенения.
В конечном итоге существование «суперциклов» солнечной активности с длительностью в несколько десятилетий или столетий было поставлено под сомнение. Скорее всего, существует нечто более длительное, протяженностью в тысячелетия. Вопрос о механизме этого явления, авторы оставляют открытым.
Но самое удивительное заключается в том, что за весь изученный период Солнце никогда не было таким активным, как за последние 60 лет. Медленное нарастание количества солнечных пятен на протяжении последних веков перешло в стремительный скачок, совпавший по времени с демографическим взрывом двадцатого столетия. Практически одновременно с этими событиями метеорологи зафиксировали признаки глобального потепления.
Правда, последние 20 лет, с 1985 года, когда был отмечен максимальный всплеск солнечной активности, она остается примерно постоянной, а потепление продолжается. Таким образом, получается, что рост солнечной активности, длившийся столетиями, а, возможно, и тысячелетиями заканчивается примерно в тот же момент времени, когда завершается последний исторический период и начинается демографический переход.
Но загадки цикличности Солнца на этом не заканчиваются. Примерно тогда же (1974– 1983 гг.) были зафиксированы колебания яркости солнечной поверхности с периодом в 160 минут[25]. Как выяснилось впоследствии, эти слабые пульсации продолжались как минимум с 1947 по 1983 гг., т.е. более тридцати лет. После 1983 года они, по-видимому, пропали. В ходе дальнейших исследований, пульсации яркости с таким же периодом были обнаружены не только у Солнца, но и у других звезд, а также у внегалактических источников (активных ядер галактик — АЯГ), что привело исследователей к идее «когерентной космической осцилляции». Из этой когерентности вытекает парадоксальный синхронизм процессов, происходящих в звездах и АЯГ, природа которых пока не ясна. Вот краткое изложение истории открытия пульсации Р0 = 160.0101 ± 0.0001 мин:
В 1976 г. советские астрономы А.Б. Северный, В.А. Котов и Т.Т. Цап на Крымской астрофизической обсерватории открыли пульсации Солнца с периодом 160.0101 ± 0.0016 мин. Пульсации эти очень слабы и охватывают все Солнце целиком. Согласно статистическому анализу временного ряда около 19 тысяч вспышек, наблюдавшихся на Солнце в 1947— 1980 гг., период пульсации Солнца Р0 = 160.0101 ± 0.0001 мин; соответствующая частота n0 = 104.1601 ± 0.0001 мкГц. Открытие было подтверждено исследователями из Станфордского университета США, причем в дальнейшем было отмечено, что колебания с таким периодом уверенно наблюдались у Солнца только в 1974—1983 гг. (Шеррер и Уилкокс, 1983; Котов, 1996).
Статистический анализ данных о частотах короткопериодических звезд показал, что не только Солнце, но и другие звезды некоторых типов также "настроены", в среднем, на эту же частоту (Котов, 1985; Котов 1997) В 1994-2005 гг. В.А. Котов и В.М. Лютый измеряя блеск ядра сейфертовской галактики NGC 4151, обнаружили колебания его яркости с периодом 160.0108(7) мин, т.е. с таким же что у Солнца. С учетом данных за 1968–1997 гг. было установлено, что период и начальная фаза осцилляций неизменны на протяжении 38 лет наблюдений за NGC 4151. Причем период этот не подвержен эффекту Доплера и не зависит от красного смещения. Такой же эффект был обнаружен и у других внегалактических объектов, самый далекий из которых квазар ЗС 454.3 (самый близкий — Солнце)
Причем удивительным оказалось распределение начальных фаз. Из 26 внегалактических объектов у 15-ти фаза совпала в пределах ошибок с фазой колебаний яркости Солнца, у 11ти, сдвинутой на полпериода, т.е. примерно половина объектов колеблется в фазе с Солнцем, а половина — в антифазе. Т.е. имеется парадоксальная согласованность колебаний яркости объектов, разделенных громадными расстояниями. Все это не укладывается в рамки обычных астрономических и физических представлений, поэтому открытые ими колебания, авторы представляют как новый космологический феномен – «когерентную космическую осцилляцию»
. [18]
Здесь мы не будем анализировать причины синхронности галактических, солнечных и земных ритмов. Влияние Солнца на Землю несомненно (работы Чижевского), но, возможно, существует и некий единый Вселенский ритм, задающий частоту и фазу для всех эволюционных процессов. [18] Если это так, то с завершением исторических циклов, которые, очевидно, не могут продолжаться за сингулярностью Дьяконова—Капицы, могут закончиться также и определяющие их инновационные волны Кондратьева, а также и синхронные с ними солнечные циклы.
Какова точность границ исторических периодов?
Она зависит от точности двух дат: момента начала неолита и точки сингулярности в формуле Форстера. Почему за начало неолита принимается 9100 лет до н.э.?
Во-первых, это именно та дата, которая хорошо соответствует алгоритму восьми шагов, и если ее изменить, то уже начало второго исторического периода будет вычислено неверно. Дело в том, что хотя неолитическая революция и представляла собой скачок, время ее начала известно с точностью до 1—2 тысяч лет. Начало же следующего исторического периода, времени появления первых цивилизаций, известно с гораздо большей точностью. Существует немало памятников той эпохи, хорошо сохранившихся до наших дней. Современные методы датировки позволяют с полной определенностью утверждать, что начался этот период примерно 3500 лет до н.э.
Действительно, все древние классические цивилизации Ближнего Востока возникли практически одновременно: объединение Египта — 3340 лет до н.э.; в Шумере первая династия Киша последовала за периодом Джемдед Наср за 3200—2900 лет до н.э.; в долине Инда хараппанская цивилизация возникла примерно за 3000 лет до н.э. В Перу недавно был обнаружен дворец возрастом 5500 лет; 3500 лет до н.э. — это 5500 лет тому назад. Значит, начало предыдущего исторического периода по алгоритму восьми шагов 5500*2 = 11000 лет тому назад или 9000 лет до н.э.
Во-вторых, эта же дата примерно 9000 лет до н.э. может быть вычислена с помощью длительности главного исторического цикла. Если принять эту длительность равной 44.4 года, что представляется наиболее правдоподобным, т.к. соответствует работам С.П. Капицы, нашей сетевой теории (42—45 лет), Кондратьевским циклам (40— 60 лет), большим солнечным циклам (44.4 года), то для момента начала неолита получаем:
256 ∙44.4 – 2022 = 9300 лет до н.э.
Вторая важная для точности вычисления границ периодов дата — это сингулярность эмпирической гиперболы демографического роста: сингулярность Дьяконова—Капицы. Для сингулярности Дьяконова—Капицы приводим нашу оценку: 2022 ± 2 года. При этом точность границ всех периодов, исключая только последний, а, возможно, и предпоследний от нее практически не зависит. Что касается последнего периода, то его конец 2022 - 44 = 1978 г. должен, вероятно, быть связан с каким-то событием, не уступающим по значимости сингулярности Дьяконова—Капицы, ведь именно в этот момент времени приходит конец цикличности исторического процесса.
Какое событие произошло в 1978 году?
Точнее, эта дата лежит в интервале 1978 ± 2 года. Но имеет ли она какое-то историческое значение? Перечислим аргументы, говорящие о том, что это так:
- 1978 год отстоит от сингулярности Дьяконова—Капицы ровно на один цикл исторического времени 2022 - 44 = 1978. В соответствии с предложенным здесь простым правилом определения границ основных исторических периодов, именно в этот момент времени завершился последний, восьмой период. После чего исторический процесс перестает быть циклическим, и наступает новая историческая эпоха.
- Именно в этот момент времени завершается четвертый экономический цикл
Кондратьева 1929—33 гг. —— 1973—75 гг. (возможно, до 1981 г.). Циклы Кондратьева
являются, видимо, главными историческими циклами, задающими основной ритм мирового
исторического процесса.
- Демографический переход, как считается, начался в шестидесятых годах двадцатого
столетия. В это время скорость роста численности населения мира достигла
максимума, и начался ее спад. Такое задание времени начала перехода соответствует
определению мультипликатора Шене и является достаточно условным. Построим в одних
координатных осях гиперболу (4):
Одну из семейства гипербол Форстера, лучше всего задающую рост численности населения мира от 40.000 г. до н.э. до 1970 г., по данным [13]. И график интерполяции зависимости численности населения мира от времени на интервале 1960-1990 гг. (International Data Base-IDB), с шагом в один год.

Рис 1С. Гипербола (4) и интерполяция демографических данных за 1960–1990 гг.
Последнее максимальное сближение, а фактически пересечение эмпирической гиперболы (4) с графиком интерполяции демографических данных произошло в 1978 году, а затем эти кривые разошлись навсегда. Поэтому, именно 1978 год можно с достаточным основанием считать моментом окончания гиперболического роста и началом демографического перехода. Согласно теории С.П. Капицы, дата начала перехода — 1965 год, при этом он занимает два цикла; момент завершения первого цикла — 2007 год, конец второго — 2049 год. Если же за момент начала перехода взять 1978 год (а именно на этот год приходится завершение последнего, восьмого исторического периода), то, во-первых, подтверждается связь исторического и демографического процессов, а, во-вторых, конец первого цикла перехода совпадает с сингулярностью Дьяконова—Капицы, приходящейся на 2022 год. Такие «совпадения» явно выигрывают в сравнении с безликими 1965 и 2007 гг. у С.П. Капицы, ведь все три даты: начало перехода, а также конец первого и второго его цикла имеют, видимо, важное историческое значение, хотя смысл его пока и неясен.
- В конце семидесятых годов прошлого века завершился гиперболический рост потребления энергоресурсов, продолжавшийся последние 140 лет.
- В семидесятые годы прошлого века остановилась в своем развитии самая фундаментальная из наук − теоретическая физика, бурно развивавшаяся до этого времени в течение более чем двух столетий. Если говорить о фундаментальных законах природы, в десятые годы XXI столетия, несмотря на все усилия, все что мы знаем об этих законах не превышает того, что мы знали о них в семидесятые XX-го. Об этом пишет в своей книге «Неприятности с физикой: взлет теории струн, упадок науки и что за этим следует» американский физик Ли Смолин.
- В это же время, т.е. в 1976.5 году, заканчивается солнечный
цикл, аналог Кондратьевского, представляющий объединение четырех (с
17-го по 20-й) одиннадцатилетних циклов. При этом совпадение с
главным историческим циклом не только по фазе, но и по длительности:
44.4 года. Такое совпадение может быть простой игрой случая, но не
стоит отбрасывать и возможность того, что оно обусловлено
синхронизмом солнечных и земных процессов, природа которого пока
неясна.
- В 1985 году, т.е. примерно в это же время, достиг своего максимума и перестал расти уровень солнечной активности, рост которого продолжался последнюю тысячу лет (или даже 11000 лет). Тогда же, 1974—1983 гг., были обнаружены малые колебания яркости поверхности Солнца с периодом, равным 1160.0101 ± 0.0016 минут, которые присутствовали в его спектре как минимум тридцать лет. Причем пропали эти колебания одновременно с завершением роста солнечной активности, продолжавшимся последние несколько столетий. Открытые в КРАО колебания представляют, видимо, новый космологический феномен: «когерентную космическую осцилляцию», а их период 160 минут — некую универсальную космологическую постоянную.
- В 1978 году численность населения Земли достигла круглого значения 232 человек. Из этого следует, что эпохи перемен наступали не просто тогда, когда эта численность удваивалась по сравнению с предыдущим периодом, а когда становилась равной 2n — двойке в некоторой целой степени. И здесь нет никакой нумерологии — это просто факт, который нужно как-то объяснять, при условии, конечно, что алгоритм восьми шагов отвечает действительности.
- Для полноты картины можно добавить также и «ненаучный» аргумент в поддержку уникальности, неповторимости и значимости того краткого момента истории конца семидесятых начала восьмидесятых годов прошлого века, о котором идет речь. Ведь именно на это время приходится пик активности НЛО, активности невиданной за всю историю наблюдений этого явления. Нечто подобное было зафиксировано еще только один раз спустя десятилетие в 1990 году.
Ответа на вопрос, что же в действительности произошло в конце семидесятых годов двадцатого века, в чем причина цикличности развития и гиперболического роста численности применяемая здесь феноменологическая схема не дает. Но можно считать, как было показано нами выше, что именно в это время (в 1978-м, а не в 1965-м году) закончился рост человечества по закону гиперболы, и начался демографический переход. И тогда же завершился последний, восьмой исторический период, а вместе с ним и циклический ход мирового исторического процесса.
Существует ли теоретическая формула
зависимости численности
населения Земли от времени?
Казалось бы, не может быть никакой теоретической формулы, описывающей гиперболический рост численности народонаселения. А постоянная Форстера и точка сингулярности гиперболы демографического роста — чисто эмпирические константы. Тем не менее, если квант исторического времени существует, алгоритм восьми шагов отвечает действительности, а в момент окончания гиперболического роста численность достигает значения 232, такую формулу легко сконструировать:
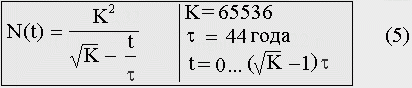
Длительность исторического цикла τ положим равной 44 года, отсчет времени ведем от начала неолита. Гиперболический рост занимает 255 циклов; в момент его окончания в 1978 году численность населения Земли достигает значения 232, и данная формула перестает правильно описывать рост. Сингулярность теоретической гиперболы, сингулярность Дьяконова—Капицы наступает в момент времени t = 256τ. Постоянная K, присутствующая в формуле, практически совпадает с безразмерной константой Капицы и связана с постоянной Форстера следующим образом:
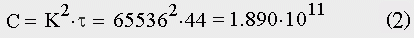
Здесь нужно отметить следующее: если алгоритм восьми шагов отвечает действительности, то постоянная K в формуле на рис. 5 г. должна быть в точности равна 65536. Действительно, в соответствии с теорией Капицы, а также и по нашей теории, произведение корня квадратного из K на τ равно продолжительности всего исторического периода развития человека, как его обычно принято определять: от неолита до наших дней. Следовательно, корень из K равен числу циклов до сингулярности Дьяконова—Капицы, т.е. 256, а К = 2562 = 65536.
Постоянная τ, единственная размерная постоянная, определяющая гиперболический рост, есть не что иное как: постоянная времени Капицы, длительность Кондратьевского цикла, продолжительность последнего, восьмого исторического периода 1934—1978 гг., учетверенная длительность одиннадцатилетнего Солнечного цикла. Это фундаментальная постоянная, задающая масштаб времени исторических изменений. Зависимость численности населения Земли от времени в соответствии с предложенной формулой на рис. 5, так же как и показатели продвижения по пути исторического развития от начала неолита до 1978 года зависели только от отношения времени t к постоянной τ, т.е. от количества циклов, пройденных Мир-системой к моменту времени t. Наиболее простой вид теоретическая гипербола приобретает в том случае, если отсчет времени вести в циклах от сингулярности Дьяконова—Капицы в прошлое:
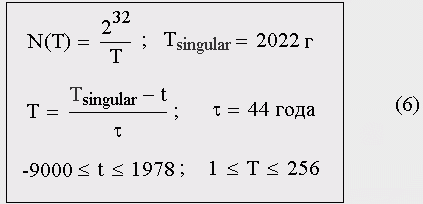
Например, чтобы подсчитать, сколько людей проживало в 1700 году, сначала вычисляем количество циклов до сингулярности Дьяконова—Капицы: (2022–1700)/44 = 7,32 цикла. Затем 4,3 миллиарда (это 232) делим на 7,32 и получаем 590 миллионов человек. Средняя длительность инновационных циклов, так же как продолжительность глобальных исторических периодов Мир-системы, выражается через фундаментальную константу исторического времени по одной и той же формуле (обобщение гипотезы Й. Шумпетера):
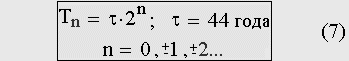
При этом продолжительность сокращающихся по закону прогрессии исторических периодов Дьяконова—Капицы может быть получена, если брать целые неотрицательные значения n в пределах от нуля до семи. Если же брать значения n большие семи, то получаются периоды эволюции рода Homo, но расположение этих периодов на оси времени не отвечает данным палеоантропологии, т.е. применяемая феноменологическая схема перестает соответствовать действительности. Отрицательные значения параметра n = -1, -2, -4 в формуле (7) задают среднюю длительность экономических циклов Кузнеца, Жугляра и Китчена.
Любопытно, что при n = -9, -11, -14 получаем, причем с приличной точностью, для продолжительности коротких инновационных циклов: месяц, неделю и сутки соответственно. При τ = 44 года цикл за номером минус четырнадцать имеет продолжительность, равную сутки с точностью до получаса, при τ = 45 лет — с точностью до четырех минут. (В заключении к книге Виктора Феллера «Предположение о структуре истории», рассмотрена схема построения исторических циклов, «атомом» в которой являются одни сутки исторического времени).
Теоретическая гипербола на рис. 5 наилучшим образом описывает рост численности населения мира от неолита до 1978 года, т.к. совпадает с эмпирической гиперболой, задающей этот рост от 40000 г. до н.э. до 1970 г. Гиперболы совпадают, т.к., во-первых, постоянная Форстера, вычисленная по формуле (2), практически равна эмпирическому значению этой постоянной. И, во-вторых, точки их сингулярности (1978 + 44 = 2022) также совпадают. Почему формула на рис. 5 столь хорошо описывает рост численности, какой циклический процесс с периодом τ задает главный исторический цикл, и что определяет константа K — все это на данном уровне феноменологии так и остается невыясненным.
Что же такое сингулярность Дьяконова—Капицы?
И.М. Дьяконов в своей книге «Пути истории» рассматривает восемь фаз или ступеней исторического процесса: первобытную, первобытнообщинную, раннюю древность, имперскую древность, средневековье, абсолютистскую средневековую, капиталистическую и посткапиталистическую. Фазы исторического развития периодизации Дьяконова хорошо соответствуют периодизации по алгоритму восьми шагов, см. таблицу 2С. Причем первобытную фазу, относящуюся к позднепалеолитическому периоду, можно считать фазой за номером нуль в теоретической периодизации; далее идут восемь исторических периодов по алгоритму и семь фаз Дьяконова. Различие в том, что в теории имеется период 1325—1674 гг., отсутствующий у И.М. Дьяконова.
И, кроме того, капиталистическая и посткапиталистическая фаза у И.М. Дьяконова ограничены 1840—1950 гг., 1952—?? гг., тогда как по алгоритму — это 1848—1934 гг., 1934—1978 гг., 1978—??гг. Что выглядит привлекательнее, т.к. эти периоды соответствуют Кондратьевским циклам. Важно отметить, что И.М. Дьяконов никогда не относился к результатам своих исследований, как к догме. Это характерно для всех его работ. Можно ли в таком случае периодизацию по алгоритму восьми шагов считать совпадающей, в пределах небольшой погрешности, с периодизацией Дьяконова? Наверное, любой ответ на этот вопрос субъективен, мы же твердо убеждены в том, что это так, столь велико совпадение независимых экспертных оценок с расчетными данными. В таком случае сингулярность Дьяконова—Капицы можно определить следующим образом:
Сингулярность Дьяконова—Капицы (историческая сингулярность) — это точка сингулярности эмпирической гиперболы демографического роста, необходимая наряду с датой начала неолита для расчета периодов мировой истории по алгоритму восьми шагов. К этой предельной точке на оси времени сходятся сокращающиеся по закону прогрессии исторические циклы. И это тот невидимый рубеж, за которым мировой исторический процесс переходит на совершенно новый, неизведанный путь развития. Исторические циклы, задававшие нарастающий темп развития человеческой цивилизации в течение последних одиннадцати тысяч лет, за сингулярностью Дьяконова—Капицы — заканчиваются. Что же нас ожидает за сингулярностью?
Несомненно только то, что с глобальными историческими циклами будет полностью покончено. Очевидно, за сингулярностью Дьяконова—Капицы их продолжение — невозможно. Но что будет с инновационными циклами? Ответить на этот вопрос, находясь на данном уровне феноменологии, невозможно, т.к. непонятна сама причина цикличности. Однако похоже, что Кондратьевский цикл каким- то непостижимым образом определяет как инновационные циклы, так и исторические. В таком случае за сингулярностью инновационных циклов также не будет.
Более того, за сингулярностью Дьяконова—Капицы могут закончиться и одиннадцатилетние солнечные циклы! Уж очень не похоже это явление на регулярный физический процесс. Достаточно вспомнить минимум Маундера, достоверность которого считается доказанной, когда в течение 70 лет с 1645 по 1715 год — пятен на Солнце практически не было совсем!
За сингулярностью Дьяконова—Капицы закончится рост численности населения Земли, а сама эта численность устремится к некоторой предельной, асимптотической величине. Этот рост численности от неолита и до нашего времени, несомненно, был связан с цикличностью исторического процесса, о чем говорит эффективность алгоритма восьми шагов, но природа этой связи на данном уровне феноменологии остается без объяснения. Ускорение развития цивилизации, связанное с ростом численности населения Земли (связь эта скорее сопутствующая, а не причинно-следственная), можно сравнить с ускорением железнодорожного состава на восьми последовательных участках трассы. Этот набор скорости будет продолжен и в ходе демографического перехода, за сингулярностью Дьяконова—Капицы, в течение еще одного цикла.
А затем во второй половине XXI века локомотив прогресса, набрав максимальную скорость, выйдет на магистраль (длина которой не определена) равномерного (не ускоренного) бескризисного развития. Отсутствие ускорения в этой метафоре означает следующее: постоянство численности населения Земли, фиксированное энергопотребление, неизменность структуры сформировавшейся ноосферы; в последовательности: мифология, этика, эстетика, искусство, наука, техника, технология, сумма технологий, ? — не будет новых членов. Причем темпы развития во всех этих областях человеческой деятельности будут максимальными, невиданными до того, так что с концом роста численности населения Земли прогресс не закончится, и творчество не исчезнет.
Но грозит ли сингулярность какими-либо катастрофами? Никаких катаклизмов, связанных с завершением цикличности исторического процесса в 2022 году, ожидать не следует. Ведь сингулярность Дьяконова—Капицы — сингулярность чисто математическая. Алгоритм восьми шагов закончил свою работу в 1978 году, но даже и тогда, в конце семидесятых годов прошлого века в момент завершения последнего исторического цикла, никаких катастроф в масштабе биосферы не наблюдалось. А ведь это было время, по значимости не уступавшее времени начала неолита и представлявшее собой сжатую до предела эпоху перемен. Есть и другие потенциальные угрозы существованию цивилизации, не связанные с окончанием цикличности исторического процесса и по странному стечению обстоятельств приходящиеся по времени как раз на сингулярность Дьяконова—Капицы. Оптимистический взгляд в будущее на все времена обеспечивает позиция финализма.
Финализм и 25 сценариев конца света
Оптимистический взгляд на ближайшие перспективы развития цивилизации — редкость в наше время. А вот в катастрофических прогнозах недостатка нет. Прежде всего, отметим и исключим мнимый кризис планетарного цикла А.Д. Панова, грозящий биосферной катастрофой в первой половине XXI века и описанный им в многочисленных публикациях. Кризис и катастрофа не состоятся по причине элементарных ошибок, допущенных Пановым — Кризис планетарного цикла А.Д. Панова — отменяется.
Катастрофические потрясения в ближайшие десятилетия предсказывает Л.М. Гиндилис в своей книге «SETI: Поиск Внеземного Разума» [14], продолжении бестселлера «Вселенная, жизнь, разум» И.С. Шкловского.
«Острота ситуации состоит в том, что коллапс должен наступить очень скоро, в первых десятилетиях XXI века. Поэтому, если бы даже человечество знало, как "повернуть" (или хотя бы приостановить) этот процесс, обладало бы средствами и волей для того, чтобы осуществить поворот уже сегодня, – у него просто не хватило бы времени, так как все негативные процессы обладают определенной инерцией, в силу которой их невозможно немедленно остановить...
Экономика Земли похожа на тяжело груженный транспорт,
который на большой скорости мчится по бездорожью прямо к бездне. Видно,
мы уже проскочили точку, где надо было свернуть, чтобы вписаться в
"траекторию поворота". И затормозить тоже не успеваем. Положение
усугубляется тем, что никто не знает, где находятся руль и тормоз. Тем
не менее и экипаж, и пассажиры настроены весьма благодушно, наивно
полагая, что, "когда понадобится", они разберутся в устройстве
транспорта и смогут совершить необходимый маневр. Не думаю, что
нарисованная картина означает непременную гибель человечества, хотя
тяжкие испытания для нас, видимо, неизбежны. Если человечество сможет
пройти через эти испытания, то характер развития должен коренным образом
измениться».
Грядущий кризис, по мнению Л.М. Гиндилиса, — это кризис, прежде всего, нехватки ресурсов по причине перехода с гиперболического роста населения Земли на экспоненциальный. Этот переход гипербола—экспонента Гиндилис постулирует. При этом причина, по которой рост человечества происходил многие тысячи лет по закону гиперболы, и которую нужно было бы понять до составления любых прогнозов, так и остается для него тайной за семью печатями..
Кроме того, теорию демографического перехода, согласно которой численность населения мира в XXI веке стабилизируется и расти больше не будет, Л.М. Гиндилис даже не рассматривает. А ведь эта теория является общепризнанной и подтверждена демографической историей стран уже прошедших переход, численность населения которых больше не растет. Ну а раз нет «коварного» экспоненциального роста, а есть «выход на полку» (асимптотическая стабилизация за счет ООС), то и катастроф никаких не будет.
При стабилизации на уровне 8—15 млрд. человек у человечества остаются в запасе многие сотни лет, чтобы разобраться с энергетическими, экологическими, экономическими, технологическими и прочими проблемами.
Близкий конец света предрекают трансгуманисты в связи с приближающейся, по их мнению, технологической сингулярностью, а также популярные писатели от науки: Алексей Турчин в книге «Война и еще 25 сценариев конца света» и Александр Никонов в книге «Верхом на бомбе». Катастрофизм Турчина носит ярко выраженный физикалистский характер:
«В основе большинства сценариев
глобальной катастрофы лежит "цепная реакция" – иначе говоря,
самоусиливающиеся процессы с нерегулируемой положительной обратной
связью. Цепная реакция позволяет с помощью малых воздействий прийти к
мощным изменениям: достаточно создать условия для возникновения
самоусиливающегося процесса.
Точно такой же принцип положительной обратной связи лежит и в основе
механизма роста населения и роста потребления ресурсов. Чем больше
население, тем быстрее оно растет, и тем больше оно потребляет ресурсов.
Однако чем больше население, тем более развитые технологии необходимы,
чтобы поддерживать его жизнедеятельность, и тем более высокие технологии
оно способно порождать, грубо говоря, за счет роста числа людей
изобретателей. Таким образом, как показал А.Коротаев, скорость роста
населения оказывается пропорциональна квадрату числа людей (dN/Dt=N∙N )
[Коротаев, 2007]. Первое N в правой части этой формулы связано с ростом
числа матерей, а второе – рост числа изобретателей. Решением этого
дифференциального уравнения является гиперболическая кривая (достигающая
бесконечности за конечное время – а именно, согласно вычислениям
Форестера, в 2026 г. [Forester, 1960]). Гиперболически растущее
население должно потреблять гиперболически увеличивающееся количество
ресурсов, что несовместимо с принципиальной конечностью ресурсов
материального мира».
Катастрофы по Турчину и демографический рост по Коротаеву обусловлены одной и той же причиной: глобальными (общецивилизационными) положительными обратными связями. Но возможно ли такое в реальности?
Турчин пишет: «Как показал Коротаев скорость роста населения оказывается пропорциональна квадрату числа людей числа людей (dN/Dt=N∙N ) [Коротаев, 2007]. Первое N в правой части этой формулы связано с ростом числа матерей, а второе – рост числа изобретателей.»
В такую интерпретацию закона гиперболического роста численности, можно только поверить, т.е. ни о каком доказательстве, конечно же, речь не идет. Модель демографического роста, разработанная Коротаевым, основана на мифе о Мир-системе по Коротаеву, т.е. на предположении о существовании главного региона, в котором всегда проживала подавляющая часть населения мира и который представлял собой единую информационную систему. И мифе об изобретателях, благодаря усердию которых и обеспечивался взрывной гиперболический рост численности, причем во все времена, для всех этносов и на всех уровнях общественного и экономического развития общества. В такое трудно поверить, впрочем, как и во все другие положения демографической теории Коротаева.
Обрисовав безрадостное будущее нашей загибающейся, погрязшей в кризисах цивилизации, Турчин, и здесь нужно отдать ему должное, задается, наконец, вопросом:
«Интересно понять, какие силы препятствуют возникновению цепных реакций (положительных обратных связей – А.М.) – ведь в большинстве случаев в реальности глобальные катастрофы не происходят или ограничены по масштабам».
Если говорить о планетарном масштабе, то за всю историю цивилизации не было ни одного катастрофического, самоусиливающегося, с нерегулируемой положительной обратной связью, процесса. Это реальность, так сказать, опытный факт. Катастрофы, конечно, случаются, но только локальные, как исключение, сбой в нормальном ходе процесса. Но если бы мир был устроен по Турчину, наша цивилизация давно бы прекратила свое существование.
Так, что же все-таки удерживает ее на плаву? Чтобы понять причины, нужно отказаться от физикалистского взгляда на прогресс и эволюцию. Ответом может быть финализм, финалистическое видение проблемы. И как проявление финализма на каждом этапе становления биосферы и ноосферы — эквифинальность циклических природных или социальных процессов, продвигающих развивающуюся систему на пути к финалу. Эквифинальность выступает здесь как особая парадоксальная системность, встроенная система интеллектуального регулирования (управления), присущая биосфере и ноосфере.
Эквифинальность — это способность биологической, социальной системы достигать целевых, финальных состояний различными путями независимо от начальных и/или текущих условий процесса. Термин эквифинальность впервые появился в биологии, а сейчас используется в медицине, экономике, менеджменте, экологии… Чем же эквифинальность биологических и социально-экономических систем отличается от гомеорезиса кибернетических систем, моделирующих первые и состоящих из подсистем, охваченных контурами отрицательных и положительных обратных связей?
Гомеорезис — это динамический гомеостазис, т.е. поддержка устойчивости, надежности динамического процесса. Это свойство относительно простых систем, которые могут быть описаны и представлены графически в виде подсистем с обратными связями. Причины же эквифинальности зачастую непонятны и загадочны и могут проявляться в виде парадоксальной системности чрезвычайно сложных объектов таких, например, как биосфера, когда существующие обратные связи столь многочисленны и сложны, что учесть их все чрезвычайно трудно или даже принципиально невозможно. Ярким примером эквифинальности на социальном уровне является экономический цикл (любой из существующих), все фазы которого реализуются в обязательном порядке, причем причины его порождающие, а точнее комплекс причин, могут находиться на совершенно разных уровнях организации общества:
«Весьма вероятно, что экономический цикл не был бы вызван к жизни если бы эти «активные» силы (изменения урожайности, изобретения, изменения в спросе и т. д.) отсутствовали или если бы изменилась одна или несколько важных черт в экономической институциональной структуре или если, например, заработная плата и условия заключения сделок были бы вполне эластичными. Если бы предприниматели вели себя каким-либо иным образом, если бы они обладали способностью безошибочного предвидения конъюнктуры или если бы организация денежной системы была другой и финансовые органы предприняли бы шаги для предотвращения последствий воздействия этих «активных» сил; словом, если бы все эти факторы действовали не так, как они действовали на самом деле». [11]
В соответствии с нашей гипотезой, рост численности населения Земли и явление экономических циклов неразрывно связаны. А именно: эквифинальность циклического развития (причиной которой является растущая по циклам сеть человека) и приводит к гиперболическому росту. Более того, не только количественные, но и качественные особенности роста: неолитическая революция, демографический переход, а также периоды исторического развития, длительность которых сжимается по закону прогрессии и все виды экономических циклов, все это объясняется одной единственной причиной — эквифинальностью главного цикла эволюции и истории (цикла фиксированной длительности, равной постоянной времени Капицы), порождающего Кондратьевский цикл.
Эквифинальность эволюции биосферы нашла свое выражение в гипотезе Геи английского ученого, инженера и мыслителем Джеймса Лавлока. [14] Согласно концепции Геи, эволюция биоты, то есть совокупности всех биологических организмов настолько тесно связана с эволюцией их физического окружения в масштабе планеты, что вместе они составляют единую саморазвивающуюся систему, которая обладает саморегуляторными свойствами, напоминающими физиологические свойства живого организма. Это НЕЧТО и было названо Геей. Весь облик Земли: климат, состав горных пород, воздуха и океанских вод есть не только результат геологических процессов, но является также и следствием присутствия жизни.
Гея как самоорганизующаяся, гомеостатическая система обладает «геофизиологическими» свойствами, т.е. поддерживает все свои параметры (температуру воздушных масс, состав атмосферы, толщину озонового слоя, состав и температуру гидросферы, почв, вулканическую деятельность, радиационный фон… — сотни параметров) в течение сотен миллионов лет на благоприятном для живых организмов уровне. Иначе говоря, биота организует как самое себя, так и параметры среды своего обитания в режиме непрерывного мониторинга и саморегуляции для обеспечения гомеостазиса или даже прогрессивного эволюционного развития. И не будь этого гомеостазиса, невозможна была бы и сама эволюция, приведшая в конечном итоге к появлению человека и его ноосферы.
Гея возникла внутри Солнечной системы и является ее частью. А Солнечная система, как результат эволюции газо-пылевого облака, оказывается удивительным образом «настроенной», причем непонятно кем, как и для каких целей — Артефакт по имени «Солнечная система». Вот примеры: равенство угловых размеров Солнца и Луны при наблюдениях с Земли; Луна всегда обращена к Земле одной стороной (резонансное вращение 1:1); правило Тициуса-Боде для орбит планет и т.д. Возникает ощущение, что какие-то неведомые силы специально «поработали» над Солнечной системой, возможно, для того, чтобы нашим потомкам было проще ее осваивать.
Но если ноосфера есть высшая стадия развития биосферы, то и вся цивилизация в целом, не страны и народы, а именно вся Мир-система, должна быть частью Геи — ее последней надстройкой, итогом, финалом ее эволюции. А если так, то ноосфера просто обязана обладать свойством парадоксальной системности Геи, что, кстати, и подтверждают парадоксальный гиперболический рост населения Земли, глобальный демографический переход, экономические и исторические циклы (циклы Дьяконова—Капицы), представляющие собой общецивилизационные согласованные процессы. Системность эта выражается также в парадоксальной эквифинальности глобального развития, которая заключается в том, что средства для достижения текущих, «плановых» целей в поэтапном, циклическом восхождении цивилизации к вершинам прогресса всегда могут быть найдены и использованы, на каком бы уровне организации природы и общества они ни находились.
В 2006 году профессор Лавлок опубликовал новую книгу, которую назвал «The Revenge of Gaia» (Гея начинает мстить), где предрекает в ближайшем будущем экологическую катастрофу. На наш взгляд, Лавлок неправомерно отделяет человека и его цивилизацию от биосферы и других «сфер»: атмо, гео... Если Гея как совокупность всех этих «сфер» была столь мудра, что ей удавалось сохранять гомеостаз в течение сотен миллионов лет, то, очевидно, с возникновением ноосферы — «сферы разума» (вершины на пути ее эволюции), ее мудрость могла только возрасти. Несомненно, экологические проблемы будут решены. Кроме того, важно понимать, что дело не в том, чтобы среда обитания оставалась совершенно неизменной, а в том, чтобы она менялась достаточно медленно, чтобы человек, как итог эволюции, успевал к ней адаптироваться.
И, разумеется, любые катастрофы пресекаются на корню, что не исключает, конечно, отдельных неудач, сбоев программы эквифинальности. Именно поэтому все надуманные сценарии конца света так никогда и не будут реализованы. Человек и его ноосфера — цель всей предшествующей эволюции, ее итог, ступень на пути к финалу, и именно поэтому они не могут быть уничтожены какой-то случайной катастрофой. Несомненно, будут еще кризисы и даже локальные катастрофы, без этого не бывает прогресса. Но почему-то не возникает сомнения, что в будущем, как и в прошлом, при участии каких-то незримых охраняющих сил, все они будут преодолены, а прогресс продолжится.
