|
Растущая иерархическая сеть Растущая ИС — это сеть, число клаттеров которой растет согласно некоторому алгоритму. Этот рост будем связывать с операцией самокопирования ИС, которая заключается в следующем: копируя текущее число клаттеров, ИС собирает новый, устанавливает в себя, прокладывает связи и увеличивает свой размер на единицу. Рост ИС начинается с двух или большего числа клаттеров.
Последовательность клаттеров, из которых собирается новый, назовем звеном цепи или просто звеном. Новый клаттер собирается в процессе копирования носителями связей каждого клаттера и его узла. Т.е. копируется каждый узел сетеобразующего клаттера и каждая входящая в него связь. Можно сформулировать иначе: с каждого клаттера копируется и устанавливается в собираемый клаттер число носителей, равное текущему размеру сети. Рост любой ИС можно условно разбить на три этапа.
Рассмотрим все эти этапы на примере сети ранга 3. Вес клаттера Р = 28 = 256, т.е. число носителей в клаттере равно 256. Корень из веса: √Р = 16. Стартовый размер сети может быть равен 2, 3 или большим. Будем считать его равным двум. Первый этап роста сети:
 Рис. 10. Старт сети 256.
Алгоритм копирования следующий: на каждую связь и на каждый узел
копируемого клаттера (узел — точка схождения связей) устанавливается
носитель. В данном случае связь одна, узел всегда один. Всего копируем
два носителя на клаттере. Нужно собрать 256 носителей, поэтому переходим
к следующему клаттеру и копируем еще два носителя. Собрали четыре
носителя. Цикл закончился, он оказался пустым, т.к. все имеющиеся на
момент входа в цикл клаттеры скопированы, а новый клаттер собрать не
удалось. Здесь мы имеем 63 пустых цикла. На 64-м цикле и 128-ой по счету
операции копирования получаем 256 носителей. Сборка третьего клаттера
заканчивается, устанавливаем его в сеть, прокладываем связи. 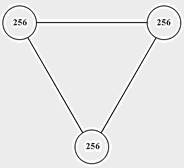 Рис. 11. Собран первый клаттер.
Теперь каждый клаттер имеет уже две связи, поэтому копируем по три носителя на клаттере или девять за цикл. Всего получается 28 пустых циклов: 28*9 = 252. На 29-м цикле копируем два клаттера, получаем остаток. Остаток отбрасываем (см. ниже) 252+3+3 = 256+2. Собираем, устанавливаем, прокладываем. 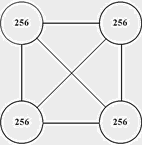 Рис. 12. Собран второй клаттер
Далее, на каждый клаттер устанавливаем 4 носителя, за цикл их собираем 16. Третий клаттер собираем за 16 циклов, т.к. 16*16 = 256. 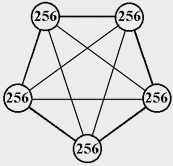 Рис. 13. Собран третий клаттер
Пять носителей на клаттер, 25 — с цикла; 10 пустых циклов: 25*10 = 250. На одиннадцатом цикле копируем 2 клаттера: 5 + 5 = 10. Берем 6 носителей и собираем новый. Здесь также получен остаток. Остаток отбрасываем (почему, см. ниже). И так далее. Доходим до 16 клаттеров. Теперь клаттер можно собрать всего за один цикл: 16*16 = 256. На этом первый этап заканчивается и начинается второй. Прирост клаттеров за цикл с этого момента идет уже по другой, как мы покажем далее, гораздо более быстрой гиперболе. Т.е. процесс роста сети претерпевает качественный скачок. Алгоритм роста при этом не меняется, а лишь дополняется правилом копирования звена и сценарием финализации цикла. 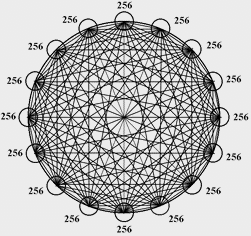 Рис. 14. Собрано 16 клаттеров.
Допустим, сеть выросла до размера 71, т.е. содержит 71 клаттер. 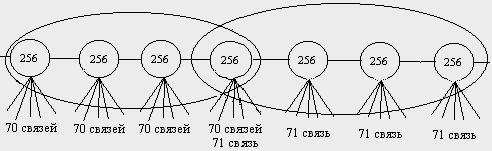 Рис. 15. Копирование фрагмента сети 256.
Для фрагмента сети, изображенного на рисунке, имеем следующее: после копирования четырех клаттеров (длина звена = 4), получаем (70 + 1)*4 = 284 носителя. Собираем новый клаттер, устанавливаем в сеть, увеличиваем число связей на единицу (71). Остаток 284–256 = 28 носителей, остается лежать на узле и связях четвертого клаттера. Процесс копирования нового звена начинаем с последнего клаттера уже откопированного, т.е. с перехлестом. 28 носителей уже лежат на позициях, их копировать не нужно. Копируем 43 + 1 = 44 позиции и переносим все носители 28 + 44 = 72 в следующий на сборке клаттер. И так далее.
Здесь важен следующий момент: в последнем копируемом клаттере первого звена возник остаток 28; формально можно его отбросить, а копирование следующего звена начать с него же и копировать с него узел и все связи — 72 позиции. Т.е. можно считать, что копирование происходит звеньями, на последнем клаттере звена остаток отбрасывается. Новое звено начинается с последнего клаттера предыдущего звена.
Дело в том, что эта математика имеет приложение, в котором носители рассматриваются как ресурс. Их остаток не может быть отброшен. Что полностью соответствует алгоритму. Действительно, в предыдущем звене с последнего клаттера было скопировано и установлено 43 носителя, в следующем звене берется остаток 28 и еще 44 (44, а не 43, т.к. была проложена связь). Получаем 43 + 28 + 44 = 115. По правилу отбрасывания остатка имеем 43 позиции с последнего клаттера предыдущего звена и 72 позиции с первого клаттера последующего звена: 43 + 72 = 115, т.е. в обоих случаях с граничного клаттера скопировано 115 позиций. Граничные клаттеры звеньев дают больший вклад (115 > 72) в дочерний клаттер, чем промежуточные. Третий этап. Когда сеть 256 достигает совершенства, ее размер (число клаттеров в сети) становится равным весу клаттера Р (числу носителей в клаттере). Алгоритм роста не может больше работать, т.к. число связей плюс узел становится равным весу клаттера, а копировать можно как минимум с двух клаттеров (в пределе с одного, но только на третьем этапе). Приступаем к заключительному этапу роста. Прежде всего, добавляем по одной свободной связи каждому клаттеру, т.е. число его связей становится равным числу носителей, в нем содержащихся. Будем считать, что максимальное число связей клаттера равно его весу.
Но, что такое связь? Можно создать ее наглядный образ, который
следует понимать только как метафору. Будем считать, что связь,
соединяющая два клаттера, подключается к некоему «мультиплексору»,
обеспечивающему независимый обмен информацией между носителями. Здесь
предполагается, что каждый носитель может быть связан в данный момент
времени только с каким-то одним носителем в другом клаттере. Для сети
256 добавочная связь на каждый клаттер, даст дополнительно 256 связей
более низкого уровня, а т.к. клаттеров всего 256, то получается 65536
связей. Все они понадобятся при построении следующей ИС более высокого
ранга. И, наконец, СИС переходит в режим репликации. Рассмотрим его подробнее. На последнем цикле роста сети длина звена, с которого собирается клаттер, становится равной двум. В процессе роста сети это число уменьшалось от 128 до 2. На последнем цикле дочерний клаттер копировался с двух, а в конце цикла — практически с одного материнского. Поэтому логично считать продолжением этого процесса операцию репликации, во время которой звено копирования минимально и равно единице, т.е. операцию, в процессе которой происходит точное копирование «клаттер в клаттер», но с установкой в новую в сеть.
Операцию репликации можно считать последней, предельной операцией самокопирования. Она состоит из одного, двух или большего числа циклов, т.е. СИС создает одну, две или несколько собственных копий. Пусть для определенности сеть создает одну копию (т.е. получается две СИС четвертого ранга). Каждая из них имеет 65536 свободных связей, две из которых идут на их (СИС) соединение. Остальные понадобятся для дальнейшего роста. Итак, сеть вышла на новый виток эволюции как ИС более высокого ранга.
Прежде чем перейти к математической реализации алгоритма роста сети, уточним понятие цикла. Цикл — это такой этап самокопирования сети, в процессе которого копируются все клаттеры, которые имеются в наличии к моменту входа в цикл. Те же из них, что собираются в текущем цикле в очередь на копирование не ставятся (исключение см. ниже). Алгоритм прохождения и финализации цикла на втором этапе роста может быть сформулирован в трех вариантах:
Рассмотрим как пример сеть, с алгоритмом роста по третьему варианту. Пусть эта сеть, содержащая 20 клаттеров ранга 3, входит в цикл. Копирование идет с 13-ти клаттеров, составляющих одно звено: 13*20 = 260 > 256, остаток отбрасываем; остается 7 + 1 = 8 неоткопированных клаттеров. Копируем их и, т.к. 8*21 = 168 > 128, заходим на второй виток и собираем еще один клаттер. На втором витке в процесс копирования будут вовлечены клаттеры, уже скопированные в данном цикле. Цикл может содержать от одного до двух витков; он может быть пустым, когда все клаттеры скопированы, а новый собрать не удалось.
Такой цикл состоит из одного звена и заканчивается на последнем
клаттере из стоящих в очередь на копирование в начале цикла. Нужно
отметить следующее: в математической модели клаттеры не обладают
индивидуальностью, здесь не нужно рандомизировать их подачу на
копирование для обеспечения эффективного кроссоверинга, достаточно
только не копировать их дважды на первом витке. При выборе алгоритма финализации цикла важно, чтобы он обеспечивал сети прохождение через все промежуточные гармонических стадии роста (с числом клаттеров, равным двойке в степени) и, конечно же, достижение в финале совершенства. Как показывает математическое моделирование, отдать предпочтение следует третьему варианту, т.к. в этом случае рост ИС проходит ближе всего к гармоническим сетям. Кроме того, выясняется, что при заданном алгоритме и при различных сценариях финализации цикла сеть проходит или «почти проходит» через все гармонические стадии роста. Т.е. они оказываются удивительно притягательными для растущей сети. Следует также отметить, что число циклов, которые проходит растущая сеть от одной точки ее роста до другой, практически не зависит от выбора сценария финализации цикла..
|
