|
Рост сети 256 Рассмотрим рост сети 256 на первом этапе от 2 клаттеров до 16. Приводим пример программы подсчета числа клаттеров за цикл в зависимости от номера цикла, реализованной в системе MathCAD: 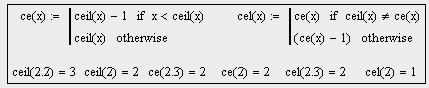 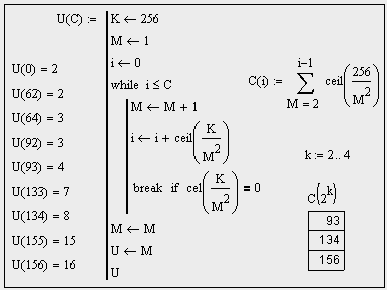 Рис. 16. Алгоритм роста сети 256 от 2 клаттеров до 16.
Здесь ceil(X) — ближайшее целое, большее или равное X, ce(X) —
ближайшее целое, меньшее или равное X, cel(X) — ближайшее целое, меньшее
X. Функция U(C) — это число клаттеров, собранных сетью за С циклов.
Например, если U(133) = 7, то за 133 цикла собрано 7 клаттеров. C(2k) —
номера циклов, соответствующие гармоническим стадиям роста сети. Всего получается 156 циклов. Из них пустых 156 - 14 = 142. Соответственно, за каждый из оставшихся 14-ти циклов собирается один клаттер. Заходить на второй виток никогда не приходится. Сеть проходит четыре гармонические стадии роста: в момент старта, а также на 93-ем, 134-ом и 156-ом цикле с числом 2, 4, 8 и 16 клаттеров, соответственно. Переходим ко второму этапу. 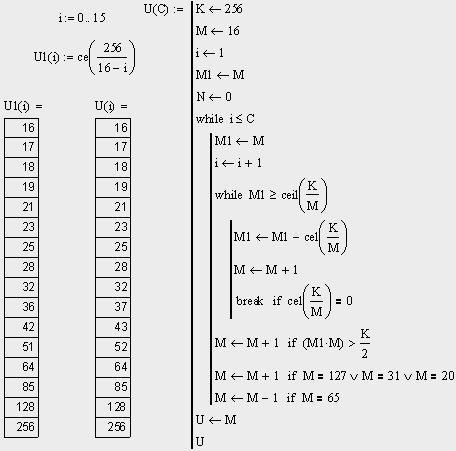 Рис. 17. Алгоритм роста сети 256 от 17 клаттеров до 256.
На этом этапе пройдено 15 циклов. Его начало сопровождается бурным
ростом числа клаттеров. Это связано с тем, что на втором этапе за цикл,
с нуля, собирается один или большее число клаттеров. Для реализации
прохода через гармонические сети понадобилась коррекция роста, но только
в четырех точках, «близких» к гармоническим сетям. Коррекция представляла собой малое возмущение в один клаттер и была проведена на стадиях роста с числом клаттеров 20, 31, 65 и 127 —> (127 + 1)*2 = 256, (31 + 1)*8 = 256, (65-1)*4 = 256. Существует не одна такая коррекция, но результат, функция U(C), — тот же. Растущая сеть проходит через гармонические стадии, с размером: 16, 32, 64, 128, 256 клаттеров. На последнем цикле число клаттеров удваивается: U(14) = 128, U(15) = 256. Этот результат справедлив для сети любого ранга. Отметим также, что результаты работы алгоритма практически полностью совпадают со значениями следующей функции: 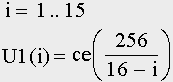 (8)
(8)Назовем функцию U1(i) теоретической гиперболой сети 256. Этап заканчивается сборкой клаттера 65536. И, наконец, третий этап роста сети 256 — репликация. Здесь сеть собирает свою копию и прокладывает связь между ней и оригиналом. Сеть 65536 может стартовать. Подведем итог для сети 256: всего имеем 156 + 15 + 1 = 172 цикла и семь гармонических стадий роста, с числом клаттеров 2, 4, 8, 16, 32, 64, 128. Последняя гармоническая сеть с числом клаттеров 256 является также совершенной.
|
