Константы Капицы

Первая из фундаментальных констант, характеризующих развитие человечества как системы — это постоянная Форстера. Как она была получена? Имея большой объем данных по численности населения Земли от Р.Х. до 1960 года, немецкий инженер австрийского происхождения Хейнц фон Ферстер (Форстер) подыскивал простую аналитическую зависимость, которая могла бы послужить неплохим приближением для имеющихся у него демографических данных. Прежде всего, он, вероятно, предположил, что численность популяции Homo sapiens, как и численность всякой другой популяции в условиях избытка ресурсов, росла
экспоненциально.

По этому простому закону, когда при удвоении численности удваивается и естественный прирост, растет все живое. Зависимость логарифма численности от времени должна быть в таком случае линейной. Когда он нанес данные на координатную плоскость, его ожидал сюрприз: график аппроксимирующей зависимости не укладывался на прямую, рост логарифма численности от времени по непонятнойпричине оказался круче линейного, и гипотеза экспоненциального роста должна была быть отброшена.

Это довольно неожиданный результат, хотя, возможно, и не слишком, ведь если вдуматься рост численности человечества, как системы высшей сложности, подверженной кризисам, войнам и эпидемиям вряд ли должен подчиняться экспоненциальному закону. Если руководствоваться здравым смыслом, то вообще трудно себе представить, чтобы этот рост можно было описать с помощью какой-то простой формулы. Априори представляется, что здесь должна быть справедлива гипотеза, близкая к нулевой. Известно, что рост происходил без спадов (возможно, за редкими исключениями), и скорость роста тоже почти всегда росла по крайней мере в среднем. Тогда зависимость численности от времени можно считать монотонно возрастающей функцией.

Но какой-то простой формулы, описывающей эту зависимость, не существует. Такой рост можно представить как суммарный рост слабо связанных подсистем: этносов, стран или народов, т.е. считать случайным процессом, и нет никакого смысла искать глобальный закон роста, справедливый для всего населения планеты, действовавший на протяжении двадцати столетий. Для каждого этапа такого, вообще говоря, случайного роста, для всех его взлетов и падений историки, социологи и демографы нашли бы, конечно, какое-нибудь естественное объяснение, и всякая математика была бы здесь бесполезна.

Возможно, так же полагал и Форстер, потерпев неудачу с гипотезой экспоненциального роста. Каким должен был быть следующий его шаг, что мог бы предпринять любой другой исследователь, попавший в подобное положение? Можно было бы попытаться подобрать полином, хорошо аппроксимирующий демографические данные, но такой полином, достаточно высокой степени, всегда можно найти и в этом нет никакого достижения… Можно попробовать в качестве кандидата степенную функцию N = C(t0 - t)n, ведь проще нее, кажется, вообще ничего нет. Собственно, так и поступил Форстер, совершенно не задумываясь о том какие причины могли вызывать такой рост, подчиненный нелинейному степенному закону.

Важно понимать, что это предположение, расходящееся со здравым смыслом и требующее большой вычислительной работы (что было совсем не просто в 1960 году!), представляется совершенно фантастическим, если не безумным. Результат точно должен был получиться отрицательным, т.е. точность для значений n и t0 должна была оказаться очень небольшой. Но совершилось чудо, эта точность, с которой определились постоянные Форстера, совершенно неожиданно оказалась чрезвычайно высокой, можно даже сказать невозможно высокой, делающей гиперболу Форстера, по сути, предзаданной.

При вычислении n по методу наименьших квадратов могло быть получено любое действительное число, например, n = -0.78 или n = -1.16, но вышло, что n = -1 с точностью до одного процента, т.е. простейший целочисленный показатель. Вряд ли целочисленность результата является всего лишь случайным совпадением. Такое совпадение возможно, но, очевидно, весьма маловероятно. Скорее всего, за этим стоит нечто большее, позволяющее говорить о населении мира как о единой системе.

И по причине этой «невозможно» высокой точности для n и t0 только и можно говорить о новой фундаментальной константе С, Форстера, характеризующей растущее человечество как систему. Нужно заметить, что сам Форстер, хотя и шутил на эту тему, но так и не понял ни причины, ни значения открытого им аномального гиперболического роста.

Рис. 1. Результаты исследования Форстером демографических данных по численности населения мира методом наименьших квадратов, I–XX в.в.

Немецкий физик Хорнер расширил время действия закона Форстера до неолита, подключив дополнительные данные, что несколько увеличило постоянную Форстера С и оставило практически без изменения n и t0 [1]:

Итак, в начале шестидесятых годов прошлого века была введена новая, видимо, фундаментальная постоянная, определяющая рост и эволюцию Homo sapiens, смысл которой для ее первооткрывателя так и остался непонятным. Размерность этой эмпирической константы, как следует из формулы Форстера, — год в степени 0.99. Что позволяет предположить, что постоянная Форстера, входящая в теоретический закон гиперболического роста, имеет размерность времени.

Заметим, что, с точки зрения теории размерностей, целочисленность показателя n имеет решающее значение. Если бы показатель n сильно отличался от минус единицы и был бы равен, например, 0.87, то размерность эмпирической постоянной Форстера выражалась бы как год в какой-то нецелой степени, и смысл ее определить было бы гораздо труднее. Но он и так остается непонятным. Что означают эти 200 миллиардов? Уж, во всяком случае, не численность народонаселения за год до сингулярности, т.к. до этой величины она точно не дорастет.

Сравним сначала законы экспоненциального и гиперболического роста численности популяции с точки зрения возможности введения в рамках этих законов характерных масштабов для времени и для численности.

Рис. 2А. Экспоненциальный и гиперболический законы роста численности популяции.

Закон, у которого не существует встроенного в этот закон масштаба для входящих в него переменных, называется масштабно инвариантным. В физике масштабная инвариантность означает неизменность уравнений, описывающих какой-либо процесс при изменении всех расстояний и промежутков времени в некоторое число раз. В теории фракталов масштабная инвариантность, самоподобие, автомодельность — это неизменность структуры фрактала при изменении масштаба.

Насколько правомерно говорить о масштабной инвариантности закона роста населения Земли, основываясь лишь на том факте, что этот рост описывается степенным законом? Возникает вопрос: масштабная инвариантность чего? Масштабная инвариантность — это неизменность уравнения или структуры. Речь, здесь явно не может идти ни о какой структуре исторического или демографического процесса во времени. Никто же не станет всерьез утверждать, что каждый из десяти исторических циклов в модели Капицы — это сжатая копия предыдущего!

Остается степенная зависимость численности от времени, которая позволяет говорить в этом смысле о законе роста населения мира, как о законе масштабно-инвариантном. Но несет ли такая масштабная инвариантность этого закона какой-либо смысл, когда даже в каузальном отношении природа его не понятна?)

В случае экспоненциального роста показатель n = 1, дифференциальный закон роста является линейным, и экспоненциальная зависимость численности от времени содержит встроенный в этот закон масштаб времени τ = 1/α. Что это означает? Это означает то, что такой рост и такой закон роста нельзя назвать масштабно-инвариантными по отношению к переменной t. Действительно, за время равное τ численность популяции всегда возрастает в 2.7 раза независимо от того, какого значения она достигла к этому моменту.

Это свойство закона экспоненциального роста популяции уникально по сравнению со всеми другими законами роста, вне зависимости от того является ли этот закон причинным, или не является, т.е. определяет положительную обратную связь между численностью и годовым естественным приростом или не определяет, а выражает лишь связь функциональную, сопутствующую. Причина уникальности — в линейности дифференциального уравнения описывающего рост, и как следствие этой линейности — независимости роста каждой части популяции от других. Следует иметь в виду, что никакого встроенного масштаба численности закон экспоненциального роста не содержит, т.к. численность за время τ возрастает, как мы уже отмечали, в 2.7 раза независимо от того, с какого значения начался ее рост.

Закон гиперболического роста (n > 1), так же как и любой другой степенной закон является, в указанном нами смысле, масштабно-инвариантным и не содержит никаких «встроенных» в этот закон масштабов времени и численности. Например, если N(t) = C∙tⁿ, и взять t₁= kt, а N₁= kⁿN, то закон роста останется неизменным: N₁= Ct₁ⁿ, т.е. он оказывается инвариантным по отношению к согласованному изменению единиц измерения времени и численности (увеличению первой в k раз, а второй в kⁿ раз.). Чего не скажешь о законе экспоненциального роста. Если N(t) = N_oe^t/^τ и взять, например, t₁= kt, то никаким изменением масштаба N₁= k₁N, закон роста к прежнему виду не привести: N₁(t) = N_o(e^t/^τ)^k → N₁(t) = No^1-k(N(t))^k ≠ k₁N(t).

Если сравнивать законы экспоненциального и гиперболического роста популяции с точки зрения характерных масштабов времени и численности, то необходимо заметить, что, независимо от их каузальной интерпретации, закон экспоненциального роста содержит «встроенный» в этот закон масштаб времени, но не содержит никакого «встроенного» в него масштаба численности. Закон же гиперболического роста, как таковой, не содержит никаких «встроенных» в этот закон масштабов времени и численности. Но если существует какой-то «сторонний», не связанный с уравнением роста масштаб, например, масштаб времени, то масштаб численности, как показал С.П. Капица, определяется с полной однозначностью из условия C = τ∙K².

Т.е. закон гиперболического (степенного) роста, в отличие от закона экспоненциального роста, либо вообще не имеет никаких характерных масштабов ни для N, ни для t, либо содержит их сразу оба. Если связь между скоростью роста и численностью населения мира является не причинно-следственной, а всего лишь сопутствующей, то должен существовать причинный закон, который обеспечивает такой рост, не являющийся в этом случае автокаталитическим процессом.

Этот же причинный закон может определять также характерное время и характерную численность, которые являются по отношении к закону гиперболического роста численности населения мира в таком случае сторонними, никак из уравнения роста не вытекающими. И, что особенно важно, так это то, что эти сторонние масштабы времени и численности являются характерными масштабами на всех этапах такого роста, в том числе на начальном его этапе, а также и во время перехода. Поэтому значения этих констант, полученные для этапа демографического перехода, могут быть использованы и при описании гиперболического роста.

С.П. Капица был первым, кто попытался выяснить смысл постоянной Форстера. Поскольку интервал времени в 200 млрд. лет для растущей популяции Homo sapiens явно не имеет никакого смысла, он представил постоянную Форстера в виде произведения двух сомножителей С = τ∙K₅. Где, согласно его подсчетам, время τ = 41—42 года и представляет собой некоторое характерное время человека.

А K₅ — безразмерная постоянная, равная примерно четырем миллиардам. Она определяет масштаб, в котором может быть измерена численность населения Земли на завершающем этапе роста. С.П. Капица представил ее как квадрат некоторой константы роста, масштаба численности в начальную эпоху роста или характерной численности К = 60000—67000, которая занимает центральное место в его теории. На вопрос, почему K₅ = K²? — феноменологическая теория Капицы ответа не дает.

«Это число занимает центральное место в теории роста, определяя все основные соотношения, возникающие при описании системной динамики человечества, являясь, в терминах синергетики, масштабным параметром. Следует отметить, что числами порядка K определяется эффективный размер группы, в которой проявляются коллективные признаки когерентного сообщества людей. Таким может быть оптимальный масштаб города или района большого города, обладающего, как правило, системной самодостаточностью. В популяционной генетике величины такого порядка определяют численность устойчиво существующего вида или популяции, занимающей определенный ареал и экологическую нишу. Иными словами, это число является масштабом сообщества, имеющего генетическую или социальную природу.» [1]

Константу K₅ С.П. Капица не вводил, а ввели ее мы, поскольку в нашей модели она играет важную роль.

Разберемся с обозначениями. Почему главное число своей теории С.П. Капица обозначил заглавной буквой K? Однозначного ответа нет, но, скорее всего, по имени автора (Kapitsa), т.к. берет заглавную K по аналогии с обозначением безразмерного числа Рейнольдса — Re, с которым Капица сравнивает свою постоянную.

Рейнольдсу было сложнее, т.к. R — универсальная газовая постоянная и пришлось взять две буквы имени Re, что привело к неоднозначности в понимании: то ли это имя переменной, то ли произведение R∙e.

Теперь о константе К₅ – почему такое странное обозначение? Дело в том, что в нашей модели рост населения мира сопоставляется росту биниальной иерархической сети четвертого ранга. Число носителей клаттера такой сети равно двойке, в показателе которой стоит также двойка в четвертой степени. Это число как раз равно постоянной Капицы K, определяющей порядок численности населения Земли на момент начала гиперболического роста. А его квадрат, K² = К₅ = 4.3 млрд., равен численности населения мира в момент начала перехода, что соответствует числу носителей структурной единицы (клаттера) сети пятого ранга.

Рис. 2В. Постоянные роста биниальных иерархических сетей от нулевого ранга до восьмого.

Для описания роста населения Земли масштаб численности K5 важен не менее, чем характерная численность Капицы K, и мы здесь это докажем.

Расщепление постоянной Форстера С на две составляющие С = τK₅ неоднозначно, и могут быть выбраны различные масштабы для времени τ и для численности K₅. Но очень важно понимать следующее: какое бы значение для K₅мы ни выбрали, характерное время τ всегда будет равно промежутку времени от момента достижения растущего населения Земли численности K₅до точки сингулярности гиперболы Форстера. Действительно, поскольку закон роста имеет вид׃ N(t) = C/(to - t) = τK₅/(to - t), то при to - t = τ → N(to - t) = K₅. Кроме того, закон гиперболического роста, записанный в характерных масштабах τ и K₅, наиболее прост по форме: N(T) = 1/T, где численность измеряется в единицах K₅, а время отсчитывается в единицах τ от точки сингулярности в прошлое.

Если исходить из общего уравнения гиперболического роста с произвольным, не обязательно целочисленным показателем n׃ N(t) = C/(to-t)ⁿ, то условие С = τ∙K₅ должно быть заменено на С = τⁿ∙K₅. Тогда закон роста приобретает вид׃ N(t) = τⁿ∙K₅/(to-t)ⁿ, и при to-t = τ, также получаем N(to-t) = K₅.

Закон гиперболического роста N = C/(to - t) — закон степенной и потому, по крайней мере, чисто формально — закон масштабно-инвариантный. Но такая его инвариантность к масштабу — не более чем промежуточная асимптотика. При выходе за границы интервала этой асимптотики, для времени и для численности появляются естественные масштабы их измерения. Во второй половине ХХ века, когда завершилась эпоха гиперболического роста, численность населения Земли составляла примерно четыре миллиарда человек.

То, что гиперболический рост завершился именно при такой, а не при какой-то меньшей или большей численности, позволяет определить ее в качестве естественной меры численности человечества на время перехода: K₅ ~ 4 млрд. Характерное время (по Капице) τ = C/K₅ будет равно промежутку времени от момента схода с гиперболы роста, т.е. от момента начала перехода до точки сингулярности гиперболы Форстера (см. выше) и составляет примерно 50 лет.

Поскольку, как было отмечено нами ранее, масштабы эти для времени и для численности являются сторонними, т.е. никак в закон степенного роста не «встроенными», их же можно принять и в качестве характерных масштабов на всех этапах роста. Ясно, что определенные таким образом характерная численность K₅ и характерное время τ являются естественными масштабами для человечества в целом как системы.

На другом конце интервала промежуточной асимптотики, в самом начале роста популяции Homo sapiens, два миллиона лет тому назад, когда численность была порядка K = 60000—70000, рост еще не был гиперболическим. При этом можно заметить, что K₅ ≈ K², и получается еще один масштаб для численности: К. Или можно даже говорить о единственной характерной численности К (как это делает С.П. Капица), которая определяет оба эти масштаба и позволяет полностью описать рост и переход.

Почему константа K₅ не менее важна для описания роста, чем постоянная Капицы К?

Действительно, постоянную К можно считать безразмерной постоянной, но можно, как полагал С.П. Капица, определить ее и как размерную постоянную. В этом случае теория размерностей позволяет избежать ошибок в процессе преобразований закона роста. С.П. Капица даже в рамках одной работы описывает константу К то как размерную, то как безразмерную. [1]

Причем полагая ее размерной, чтобы добиться равенства размерностей в правой и левой части уравнения Капицы, он даже вводит две константы К, равные по величине, но одну из них считает безразмерной, а вторую с размерностью численности! [21] На самом деле, вводить две константы нет никакой необходимости, ведь если считать, что K5 имеет размерность численности — проблема полностью снимается. Постоянная К в таком случае имеет размерность корень квадратный из размерности численности.

Рис. 3. Расщепление постоянной Форстера С на константы Капицы К и τ.

Масштаб времени или характерное время τ, которое, как было показано нами ранее, должно составлять примерно 50 лет, С.П. Капица уточнил следующим образом. Он добавил член τ² в знаменатель выражения для скорости изменения численности (1), а затем, проинтегрировав его, получил одну из ряда возможных гладких, с «выходом на полку» кривых, описывающих изменение численности во время перехода. В результате сингулярность пропала, и можно было сравнивать фактические данные по населению мира на конец ХХ века и по формуле (2). Испробовав семь вариантов с τ = 20, 25, 33, 40, 42, 45, 55 лет, С.П. Капица пришел к выводу, что наилучшее приближение дает вариант № 5 с τ = 42 года.

Рис. 4. Определение характерного времени τ путем замены гиперболы на время демографического перехода гладкой кривой с горизонтальной асимптотой.

Важно понимать следующее: вычислить постоянные роста оказалось возможным по двум причинам. Первая причина заключается в том, что рост на протяжении тысячелетий описывался, причем с очень высокой точностью, простейшей из возможных, степенной гиперболической функцией. (В модели Капицы при to - t >> τ уравнение (2) по идее должно описывать гиперболу Форстера.) Именно поэтому Форстером была получена с хорошей точностью его постоянная С.

А вторая следует из теории глобального демографического перехода, в соответствии с которой этот рост, длившийся тысячелетиями, за ничтожное по историческим меркам время во второй половине текущего столетия, т.е. практически мгновенно, прекращается, численность стабилизируется (в модели Капицы устремляется к асимптоте кривой (2)) и меняться больше не будет. Как показывает анализ демографического перехода, мы в данный момент времени (второе десятилетие XXI века) приближаемся к его середине, причем длительность перехода составит примерно 100 лет.

Т.е. стабилизация численности произойдет не за 10000, не за 1000 и не за 500 лет, а именно за 100 лет. Момент отхода закона роста от гиперболы Форстера, численность в этот момент времени, длительность первого цикла перехода от момента его начала до сингулярности гиперболы Форстера, динамика роста численности в конце ХХ, начале XXI века — все эти данные позволили «расщепить» постоянную Форстера на константы Капицы.

Действие своих констант, полученных при анализе начала перехода, С.П. Капица распространил и на эпоху гиперболического роста. В своих работах он утверждает, что именно такой масштаб времени характеризует также и процесс гиперболического роста населения мира, продолжавшегося тысячи или даже десятки и сотни тысяч лет. И для этого есть все основания. Так, характерная численность человеческих поселений, районов в составе большого города составляет как раз К человек, а характерное время τ равно усредненной продолжительности человеческой жизни; этому же значению равна длительность Кондратьевского цикла, который считается, по мнению ряда исследователей, главным циклом истории и экономики.

Демографический переход, согласно теории Капицы, укладывается в удвоенное характерное время: 2τ = 2(42—45) ~ 100 лет. Оба эти явления: гиперболический рост и демографический переход до сих пор остаются во многом непонятными и загадочными, и оба эти явления позволили С.П. Капице смоделировать рост с помощью кривой (2) и подсчитать постоянные К и τ.

Описание С.П. Капицей роста и перехода, в рамках своей модели, содержит ряд непонятных моментов. Так, уравнение (2) он, очевидно, считает экстраполяцией гиперболы роста на эпоху перехода. С этим трудно согласиться, т.к. уравнение (1) было получено в результате нескольких последовательных изменений (можно даже сказать искажений) из уравнения гиперболы Форстера рис. (1). Действительно: во-первых, для показателя n степенной функции автор берет не усредненное значение n = -0.99 по Форстеру, а целочисленное n = -1. Такая подмена, как мы это покажем в дальнейшем, существенно повлияла на точность в определении им постоянных К и τ.

Во-вторых, при выборе экстраполирующей функции (2), С.П. Капица варьирует не только характерное время τ, но также постоянную Форстера С (в формуле (1) стоит С' = 186 (163) млрд., а не С = 179 млрд., как у Форстера), а также и to, которое у него 2007 (1995) г., а не 2027 г., как у Форстера. В результате его арккотангенсоида, описывающая рост за последние 250 лет, оказывается слабо связанной с гиперболой Форстера.

Да и есть ли такая связь вообще? Всегда ведь можно подобрать достаточно гладкую кривую (например, с помощью полинома), хорошо отвечающую демографическим данным за последние два с половиной столетия. Что же касается предшествующих им семнадцати с половиной веков, ясно, что эта арккотангенсоида не согласуется с демографическими данными и не совпадает с гиперболой Форстера, т.к. C' ≠ C.

Возможно такое возражение: С'=186 млрд., а не С=179 млрд., как у Форстера, но разница невелика, а с учетом того, что точность демографических данных быстро убывает (составляет десятки процентов) по мере ухода в прошлое, можно ли вообще говорить о каком-то несовпадении С и С'? Ответ такой: для оценки численности населения мира в любой момент времени от 0 до 1960 года, можно считать, и это будет нормально, что n = -1, а не -0.99, а константу С взять равной 179, 186 или даже 200 млрд. Но если мы хотим определить c максимально возможной точностью постоянные К и τ, которые являются интегральными характеристиками роста, т.е. определяют его на протяжении двадцати столетий, нужно использовать средние значения, полученные Форстером, т.е. тройку [C = 179, n = -0.99, to = 2027], не меняя в ней ни одну из величин.

Можно ли в таком случае доверять полученным результатам К = 67000, τ = 42 года? Здесь еще нужно учесть то, что постоянные n, С и to согласованы и нельзя произвольно, даже в небольших пределах изменять их по отдельности, а также и то, что условие К2τ = C, связывающее константы Капицы, должно быть уточнено, см. ниже. Кроме того, примерно такой же по точности результат может быть получен, как это было сделано нами ранее, гораздо более простым способом, исходя лишь из того факта, что численность в момент начала перехода была равна K5, а характерное время τ равно интервалу времени от начала перехода до сингулярности гиперболы Форстера.

Еще один непонятный момент связан с тем, что константы К и τ С.П. Капица вводит и вычисляет на момент начала перехода, а затем эти же постоянные применяет и при описании гиперболического роста, используя их в уравнении Капицы. Что, как мы отмечали ранее, вполне законно, если считать эти постоянные сторонними по отношению к закону степенного роста. Но это противоречит основной предпосылке его модели о самоподобии роста, его масштабной инвариантности, когда в эпоху гиперболического роста нет, и не может существовать никаких характерных масштабов τ и К для времени и для численности.

Масштабная константа K₅, константа Капицы К, которую он считал главным параметром своей модели определяют характерный масштаб численности населения, и уже поэтому полагать, что степенная зависимость N = C∙(to-t)^-1, описывает самоподобный, масштабно-инвариантный процесс роста населения Земли [1] — представляется ошибочным.

То же можно сказать и о характерном времени τ = 42—45 лет, если считать его системным, т.е. характеризующем систему «растущее население Земли». Но если считать, что оно характеризует лишь носителя цивилизации, человека, тогда масштабная инвариантность закона N = C∙(to-t)^-1, как, вероятно, полагал С.П. Капица, будет выполняться. С этим вряд ли можно согласиться.

Даты и численность согласно теории		Исторические и антропологические данные
1	Сетевая модель: Время эволюции человека. (появления рода HOMO): T_evol = 42397τ = 1.85 млн. лет Численность первых гоминид N ~ K = 65536. Модель С.П. Капицы: T=(π/2-1)Kτ=1.6 млн. лет, N ~ K = 60000-67000	Первые архантропы (гоминиды периода 1800 – 400 тыс.л.) появились в Африке, Азии, Грузии... примерно 1,9 млн. лет назад. Численность первых гоминид N ~ 100000.
2	Время начала неолита: T_neol = -√Кτ = -9000 лет Численность N ~ K√К = 17 млн. чел. (Обе модели.)	Неолитический период начался 10-12 тыс. лет тому назад. Численность N ~ 10 млн. чел.
3	Сокращающиеся по закону прогрессии циклы эволюции и истории, продолжительность которых после неолита составляет √Кτ/2ⁿ, n=1...8 (Обе модели.)	Исторические данные полностью соответствуют алгоритму восьми шагов.
4	Сетевая модель: Время начала перехода t = -τ = -44 года от сингулярности или 1978 год от р.х. Длительность перехода Тп = 2τ~100 лет. Численность на момент начала перехода N = K² = 4.3 млрд., на момент завершения перехода 2K² = 8.6 млрд. Модель С.П. Капицы: Длительность перехода Тп = 2τ~100 лет. Численность на момент завершения перехода N = 2K² - 3K².	Данные по демографическому переходу будут получены во второй половине XXI столетия.

Таблица 1. Самые важные даты эволюции и истории человечества, рассчитанные теоретически с помощью постоянных Капицы τ и К. Приведены современные научные данные по численности населения Земли в эти моменты времени.

Результаты расчетов в рамках первой и второй модели в первом приближении совпадают и полностью соответствуют данным демографии, истории и палеоантропологии — таб. 1. Все это указывает на то, что τ и К — фундаментальные постоянные эволюции человека. Кроме того, об этом же говорит и полученная нами теоретическая зависимость численности от времени (5), полностью совпадающая с эмпирической гиперболой, описывающей рост населения Земли за последние сорок с лишним тысяч лет.

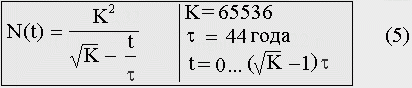
Рис. 5. Теоретическая гипербола, совпадающая с эмпирической гиперболой демографического роста. Отсчет времени ведется от момента начала неолита.

Если бы константы τ и К не были постоянными эволюции человека — не было бы и никакой теоретической зависимости, описывающей гиперболический рост населения мира. Если же считать, что квант исторического времени, точнее, его цикл (т.е. абсолютная разметка исторического времени на периоды постоянной длительности), существует, алгоритм восьми шагов отвечает действительности, такую формулу легко получить.

Длительность исторического цикла τ здесь равна 44-м годам, отсчет времени ведется от начала неолита. Гиперболический рост занимает 255 циклов, в 1978 году численность населения Земли достигает 2³², и формула (5) перестает работать. Сингулярность теоретической гиперболы Дьяконова-Капицы наступает в момент времени t = 256τ.

В физике, как правило, безразмерные постоянные появляются в качестве эмпирических параметров, а затем находят свое объяснение при развитии физической теории. Здесь похожая ситуация: т.к. К безразмерная константа и не зависит от системы единиц, то ее значение должно, так или иначе, следовать из несуществующей пока теории эволюции человека или даже будущей теории универсальной эволюции.
И здесь есть согласие феноменологической теории Капицы и сетевой модели: постоянная К, равная двойке в шестнадцатой степени в нашей теоретической схеме (возможно, являющейся первым шагом на пути к созданию такой теории), практически совпадает с безразмерной константой феноменологической теории Капицы.

Постоянная τ, единственная эмпирическая размерная константа, определяющая гиперболический рост, есть не что иное, как постоянная времени Капицы, длительность Кондратьевского цикла, продолжительность последнего, восьмого, исторического периода 1934–1978 гг., половина длительности демографического перехода. Это фундаментальная постоянная, задающая масштаб времени исторических изменений.

Численность населения Земли как функция времени в соответствии с формулой на рис. 5, так же как и показатели продвижения по пути исторического развития от начала неолита до 1978 года, зависела только от отношения времени t к постоянной τ, т.е. от количества циклов, пройденных Мир-системой к моменту времени t. Наиболее простой вид теоретическая гипербола на рис. 5 приобретает тогда, когда отсчет времени ведется в циклах от сингулярности Дьяконова—Капицы в прошлое:

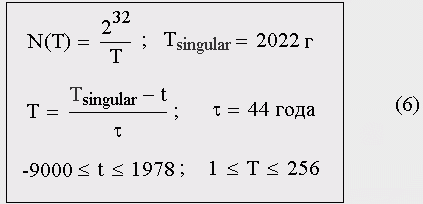
Рис. 6. Наиболее простой вид теоретической гиперболической зависимости численности населения мира от времени. Отсчет времени ведется от сингулярности гиперболы в прошлое.

Например, чтобы подсчитать, сколько людей проживало в 1700 году, сначала вычисляем количество циклов до сингулярности Дьяконова—Капицы: (2022 - 1700)/44 = 7,32 цикла. Затем 4,3 миллиарда — это 2³² делим на 7,32 и получаем 590 миллионов человек.

Средняя длительность инновационных циклов, так же как продолжительность глобальных исторических периодов Мир-системы, в нашей модели выражаются через фундаментальную константу исторического времени по одной и той же формуле:

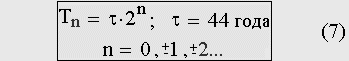
Рис. 7. Обобщение гипотезы Шумпетера. Формула, выражающая продолжительность сокращающихся по закону прогрессии циклов Дьяконова—Капицы от начала неолита до конца ХХ века через фундаментальную постоянную эволюции — постоянную времени Капицы.

При этом целые неотрицательные значения n берутся в пределах от нуля до семи. Отрицательные значения параметра n: n = -1,-2,-4 задают среднюю длительность экономических циклов Кузнеца, Жугляра и Китчена. Любопытно, что при n = -9,-11,-14, получаем, причем с приличной точностью, для продолжительности коротких инновационных циклов: месяц, неделю и сутки соответственно. При τ = 44 года цикл за номером минус четырнадцать имеет продолжительность равную сутки с точностью до получаса, при τ = 45 лет — с точностью до четырех минут. Вывод: Таблица 1, Зависимости (5) и (7) говорят о том, что постоянные Капицы τ и К — фундаментальные константы эволюции человека.

В заключении книги Виктора Феллера «Предположение о структуре истории» рассмотрена схема построения исторических циклов, «атомом» в которой являются одни сутки исторического времени. Возможно это случайное совпадение, но нельзя не отметить, что продолжительность инновационных циклов и циклов Дьяконова-Капицы может быть получена простым умножением времени обращения Земли вокруг своей оси в наше время (с момента своего возникновения 4.5 млрд. лет назад из-за приливных сил Земля постоянно замедляла свое вращение) на двойку в некоторой целой степени.

Эволюцию физической картины мира можно рассматривать как переход от физики без фундаментальных констант (классическая физика) к физике с фундаментальными константами (современная физика). Подобно тому, как с каждой новой физической теорией связана фундаментальная физическая постоянная (с, h), с новой теорией эволюции также могут быть связаны фундаментальные постоянные эволюции. Возможно, новая теория эволюции в отличие от классической, на основе естественного отбора, будет включать константы τ, К, to или производные от них для эволюции человека и для универсальной эволюции вообще.

И подобно тому, как фундаментальные физические постоянные не просто фигурируют как коэффициенты в физических законах, а определяют границы применимости физических теорий, константы эволюции определяют границы по времени и по численности, в которых происходит рост населения мира и эволюция человека. Это в первую очередь касается численности населения Земли в трех главных точках ее роста, жестко закрепленных на оси времени и связанных, согласно нашей гипотезе, с датой to.

Первая точка ~ 2 млн. лет тому назад — это начало роста, когда появился род Homo и стартовал гиперболический рост численности наших далеких предков; тогда она по порядку величины была равна К. Вторая точка — момент начала неолита, когда она стала равной К√К. И, наконец, третья точка — это момент начала перехода, когда численность стала равной К2. Константы τ, К и to определяют в модели Капицы и в нашей модели как границы по времени для эволюции человека [-2млн. лет, 2100 г. н.э.], так и границы по численности на этом интервале времени [2К, ~2К2]. При удалении в прошлое на времена большие, чем 2 млн. лет или в будущее в XXII столетие и далее, константы τ и К не могут уже считаться постоянными эволюции человека и присутствовать в законе роста численности.

Даты, отмечающие начало роста, его середину на логарифмической шкале времени и его конец, по нашему твердому убеждению, так же как и постоянные Капицы, должны занять свое место среди постоянных эволюции человека. Для исторического процесса особую важность представляют первая и вторая демографическая революция: моменты начала взрывного роста численности населения мира и взрывной ее стабилизации на предопределенном уровне. В модели С.П. Капицы неолитический период никак не выделен, отмечается лишь [3,4], что неолит приходится точно на середину исторического времени, пересчитанного в логарифмическом масштабе. А ведь именно во время неолита, и это считается общепризнанным, стартовал тот процесс, который ныне называется историческим.

И если начало истории — это начало неолита, то ее (по крайней мере, в том виде, в каком мы ее знаем) конец — это вторая за всю историю человечества демографическая революция: демографический переход.

Вот только один пример, говорящий о том, что что мир, в котором будут жить наши дети и внуки, будет кардинально отличаться от того, каким мы его знали на протяжении последних сотен лет.

Который С.П. Капица справедливо называет периодом коренной ломки всех установившихся в течение тысячелетий способов развития: «Демографическая революция и переход к постоянному населению, несомненно, самое крупное за всю историю потрясение в развитии человечества» [21].

Демографический переход, внутри которого все мы находимся, начался во второй половине ХХ столетия и закончится во второй половине XXI-ого. Но существует ли какая-то конкретная дата, точка на оси времени, которую можно было бы связать с этим переходом?

Казалось бы, что может быть естественнее, чем связать с эпохой демографического перехода сингулярность эмпирической гиперболы демографического роста? Это та дата, при приближении к которой численность населения мира устремляется к бесконечности при условии неизменности закона роста. Если есть гипербола роста, продолжавшегося в течение тысячелетий, то существует и точка ее сингулярности, при подходе к которой рост этот, несомненно, должен претерпеть некие качественные изменения. И у этой точки на оси времени должен быть какой-то смысл.

Однако, как это ни странно в построениях С.П. Капицы эта дата вообще отсутствует. Вместо 2025 года он вводит какую-то "безликую", ни о чем не говорящую дату: 2007 год, когда, согласно первому варианту его модели, скорость роста должна была достичь максимума: «Скорость роста пройдет через максимум при Т₁ = 2007 г.... Из-за введения τ значение критической даты максимума Т₁ сдвигается от 2025 года к 2007 году. Этот сдвиг, который следует ожидать, и который в физике связывают с перенормировкой». [1] Когда выяснилось, что максимум скорости роста населения мира был достигнут в 2000 году, С.П. Капица передвинул этот бессмысленный «полюс» на 1995 год [21] .

Смысл этой точки сингулярности, как нам представляется, не связан с какими-то конкретными событиями истории, экономики или демографии, которые непременно должно произойти в двадцатых годах текущего столетия. А в том, что эта дата, так же как и дата начала неолита, представляет своеобразную отметку на оси времени, которая позволяет разметить историю человечества на восемь сокращающихся по закону прогрессии исторических периодов. Алгоритм такого разбиения, алгоритм восьми шагов, очень прост: делим отрезок времени от начала неолита до сингулярности гиперболы Форстера пополам, затем делим пополам оставшуюся половинку, ту, что у сингулярности. И так восемь раз. В итоге получаем восемь сокращающихся по закону прогрессии исторических циклов.

Можно по-разному относиться к феноменологической теории Капицы, но одно несомненно: введенные им постоянные позволяют рассчитать с прекрасной точностью важные даты и циклы как истории, так и эволюции, а также численность населения мира во все времена. С.П. Капица и сам с некоторой растерянностью отмечал этот удивительный и непонятный феномен. Феномен, который становится еще более удивительным, если учесть, что наша модель, идейно никак не связанная с моделью С.П. Капицы, оказывается полностью ей изоморфной.

Т.е. использует (без всякой подгонки) те же самые константы, но в совершенно иной их интерпретации, и выдает практически те же самые результаты. Ясно, что могут быть построены новые модели, могут быть уточнены старые. Может быть предложена иная, отличная от существующих интерпретация постоянных Капицы. В одном только нет сомнения: постоянные К и τ — фундаментальные постоянные эволюции человека.

Может оказаться так, что постоянные Капицы имеют очень простой смысл. Так, константа К в нашей модели — это 2¹⁶, а константа τ, возможно, будет выражена через планковское время. Так это или не так — покажет только время. Действительный смысл постоянных τ и К сможет прояснить лишь новая теория эволюции.

К вопросу о точности, с которой определены постоянные гиперболического роста n, τ, К, to

Здесь мы попытаемся ответить на два важных вопроса, касающихся постоянных роста:

Действительно ли показатель степенной функции в законе Форстера в точности равен минус единице?

Можно ли было определить константы τ и К с большей точностью по сравнению с той, какая была получена С.П. Капицей?

Прежде всего, необходимо обратить внимание на разницу, существующую между теоретической и эмпирической зависимостью. Невозможно оспаривать результаты эмпирического исследования Форстера и, в частности, значение осредненного за двадцать столетий показателя n = -0.99. Утверждение о том, что значение показателя степенной функции в законе Форстера должно быть в точности равно минус единице относится к теоретической зависимости численности населения мира от времени, отражением которой и являются результаты эмпирического исследования Форстера (рис. 1.) Зависимости, которая возникла в результате непрерывной работы неизвестного и по настоящее время динамического причинного закона.

В рамках нашей модели такая теоретическая зависимость найдена, но ею нельзя воспользоваться, т.к. неизвестны с достаточной точностью момент начала неолита и характерное время τ.

Таким образом, говоря о законе роста, законе Форстера, гиперболе Форстера, мы имеем в виду теоретический закон гиперболического роста.

Гиперболической зависимостью называется любая степенная зависимость вида Y = CXⁿ, где n < 0 и не обязательно целое. Является ли показатель n в законе Форстера целочисленным, или же он может быть равен какому-то другому, близкому к минус единице значению? Это очень важный вопрос, т.к. точность, с которой Форстер определил его в своей работе, некоторыми авторами ставится под сомнение.

Рис. 1. Результаты исследования Форстером демографических данных по

численности населения мира методом наименьших квадратов I - XX в.в.

Такое искажение исследования Форстера позволяет им говорить не о законе гиперболического роста, а о гиперболическом тренде, предлагать теории роста, способные объяснить лишь такой гиперболический тренд, но никак не закон и называть гиперболический рост населения Земли «надэкспоненциальным». Что гораздо лучше отвечает их редукционистским моделям, не способным объяснить парадоксальную системность растущего человечества. Так, С.В. Цирель в своей тяжелой для восприятия, наукообразной статье "Скорость эволюции: пульсирующая, замедляющаяся, ускоряющаяся", пишет:

«Дальнейшие исследования (Kremer 1993; Коротаев 2006; Цирель 2008) показали, что сама пропорциональность выполняется не столь жестко, что показатель степени в знаменателе не обязательно равен единице и не обязательно неизменен в течение всей истории человечества, поэтому предопределенность, заданная уравнением (1), (эмпирической гиперболой Форстера [А.М.]) существенно преувеличена.»

И даже С.П. Капица выражает сомнение в точности, полученной Форстером для показателя n:

«Заметим, что точность определения показателя n представляется несколько преувеличенной.» [1]

Здесь мы приведем аргументы, говорящие о том, что показатель n в формуле степенного закона роста численности населения мира от времени должен быть в точности равен минус единице. Иначе говоря, имея для показателя степенной функции при обработке данных по методу наименьших квадратов столь точный и столь близкий к минус единице результат, можно было сразу же прийти к утверждению о том, что в формуле закона, вызывающего такой рост, показатель n должен быть в точности равен -1 и не может быть равен, например, -0.99 по принципиальным соображениям. Мы докажем, что целочисленное значение показателя n = -1 занимает выделенное по сравнению с другими, близкими к минус единице действительными значениями, его соседями на числовой оси.

Действительно, если считать, что в законе роста показатель n ≠ -1, а равен, например, -0.99, то размерность постоянной Форстера С, как это следует из закона Форстера, учитывая, что N безразмерная величина, не будет уже иметь размерность времени, а будет иметь какую-то непонятную размерность: год или секунда в степени 0.99. Что вряд ли может считаться приемлемым, т.к. эта константа определяла рост населения Земли на протяжении многих тысячелетий и, несомненно, является фундаментальной постоянной роста и развития человечества.

И подобно тому как все фундаментальные физические постоянные имеют размерность, выражающуюся в целых или полуцелых степенях основных единиц измерения, постоянная Форстера С не может иметь размерность [T]^0.99. Она должна иметь размерность времени. Поэтому недопустимо даже небольшое отклонение n от минус единицы, иначе придется признать эту размерность переменной, т.к. по мере поступления новых данных и уточнения закона, она будет изменяться.

Здесь может быть такое возражение. Допустим n = -1-α, тогда N = C/(to-t)^(1+α), и если константу С представить в виде: C = C₁∙τ₁^(1+α), закон роста будет иметь вид: N =C ₁(τ₁/to-t)^)1+α, где C₁— безразмерная константа, а τ₁ имеет размерность времени. Что, казалось бы, как-то решает проблему размерности времени с нецелочисленным показателем.

Но дело в том, что если считать закон степенного роста законом масштабно-инвариантным (а так считают почти все исследователи гиперболического роста, включая С.П. Капицу), то для него не существует никакого встроенного масштаба времени τ_1,, а значит константы C₁ и τ₁— произвольны (при условии C₁∙τ₁^(1+α) = C) и не имеют никакого демографического, эволюционного и исторического смысла. Следовательно, опять приходим к тому, что постоянная С, с непонятной размерностью является фундаментальной константой роста населения Земли.

Но даже если признавать существование сторонних, не связанных со степенным законом роста, масштабов времени и численности (как это делает, например, С.П. Капица), вряд ли может считаться приемлемым сам вид такого степенного закона, в показателе которого стоит значение близкое к минус единице, например, -0.99, да еще и уточняющееся по мере поступления новых данных. Выход здесь один: α = 0.

Рис. 3. Расщепление постоянной Форстера С на константы Капицы К и τ.

Если бы в результате вычислений, которые провел Форстер, показатель n оказался нецелым и далеким от -1, и если бы точность его оказалось не столь высока, то, учитывая большой объем данных, используемых им в своей работе, можно было бы сделать вывод о том, что аппроксимация закона роста степенной функцией не может считаться удовлетворительной. В таком случае не было бы никакого закона степенного роста населения Земли, не было бы никакой постоянной роста и не возникало бы никакого вопроса о ее размерности. Закон роста в таком случае мог быть каким-то иным, возможно, экспоненциальным, или даже это мог быть какой-то случайный процесс.

Если же n оказался близок к минус единице, но не равен ей (n ≠ -1), близок в том смысле, что в результате обработки большого объема данных доверительный интервал для него оказался небольшим и включающим целочисленный показатель, в данном случае -1, то соображения размерности позволили бы сразу же считать этот показатель в точности равным -1. Иначе пришлось бы вводить фундаментальную константу с непонятной и переменной размерностью. У Форстера n = [-0,999, -0,981] и интервал немного, на одну тысячную, «не дотягивает» до -1, но все равно нужно положить n = -1, т.к. его границы выбираются по предзаданной вероятности.

Вывод здесь простой: закон роста населения Земли не мог быть «примерно» гиперболическим с нецелым n, близким к минус единице, и говорить о гиперболическом тренде, гиперболической тенденции и «надэкспоненциальном росте» в применении к мировому демографическому процессу — неверно в принципе.

И еще один важный момент. Что означает утверждение о том, что в течение всей эпохи гиперболического роста показатель n в законе роста был равен минус единице? Оно не означает, конечно, что рост всегда шел в точности по гиперболе Форстера, что естественный прирост населения мира причинно определялся численностью и был в любой момент времени равен ее квадрату, деленному на постоянную Форстера. Даже если бы это было так — рост все равно не был бы гиперболическим по причине его неустойчивости.

По нашему мнению, такой рост может быть представлен как нестационарный случайный процесс, похожий на случайное блуждание по вертикали, направленное на гиперболу роста, с постоянным дрейфом по горизонтали в координатах время-численность на графике гиперболы демографического роста. Показатель n в законе роста в таком случае в точности равен минус единице лишь в том смысле, что это случайное блуждание во все времена каким-то непонятным образом направлялось на теоретическую гиперболу демографического роста, у которой n = -1. Именно поэтому при обработке данных по методу наименьших квадратов усредненный показатель n и оказался столь близок к минус единице.

Итак, почему n = -1? Тому есть две причины:

Работа Форстера, результаты которой считаются общепризнанными, из которой следует, что n = -1 с точностью до одного процента.

Соображения размерности: постоянная Форстера должна иметь размерность времени, а это возможно лишь при n = -1.

Теперь о потере точности при определении С.П. Капицей постоянных τ и К. По нашему мнению, такая потеря произошла при замене n = -0.99 (усредненный показатель по Форстеру) на целочисленный показатель n = -1. «Как же так!» — возможно, удивится читатель. Только что доказали, что показатель n в законе Форстера должен быть в точности равен -1, а теперь утверждаем обратное?

Рис. 1А. Результаты исследования Форстером демографических данных по численности населения мира методом наименьших квадратов, I–XX в.в.

Противоречия здесь нет, т.к. причинный динамический закон, благодаря которому эмпирический закон роста численности от времени оказался столь близок к гиперболическому с n = -1, предполагает существование теоретической гиперболы, показатель которой в точности равен минус единице. Говоря о законе Форстера, мы и имеем в виду эту теоретическую, «идеальную» гиперболу.

Но при подсчете постоянных τ и К нужно пользоваться не теоретическим, а эмпирическим законом, т.е. гиперболической зависимостью с показателем 0.99. Сейчас мы это докажем, но прежде всего дадим четкое определение характерным масштабам численности и времени, K5 и τ:

Примем за естественную меру для переменной «численность населения Земли» полное число живущих на тот момент времени, когда завершилась эпоха гиперболического роста и начался демографический переход. Иначе говоря, K₅ — это численность населения мира в тот год, когда закон роста, остававшийся неизменным в течение многих тысяч лет, навсегда отошел от гиперболы.

В качестве масштаба времени выберем интервал времени, отсчитываемый от момента начала демографического перехода до точки сингулярности гиперболы демографического роста. Назовем этот интервал времени τ — характерным временем исторических изменений.

Момент времени, отмечающий завершение эпохи гиперболического роста, трудно определить по следующим причинам: во-первых, численность населения мира во второй половине XX века известна с точностью всего лишь в единицы процентов. И, во-вторых, если исходить из нашей модели, гиперболический рост населения Земли, хотя и представляет собой рост управляемый, подчиняющийся условию эквифинальности, тем не менее является по своей природе процессом случайным, что также отражается на точности при выборе момента отхода закона роста от гиперболы.

Выбор таких масштабов вполне логичен, т.к. оба они характеризуют систему «растущее человечество» во время демографического перехода. И, т.к. эти масштабы, очевидно, являются сторонними, не «встроенными» в степенной закон роста численности от времени (порожденными той же самой «внешней» причиной, которая определяла рост по гиперболе), то можно распространить их действия и на эпоху гиперболического роста.

Найти значения этих масштабов можно исходя из данного определения, однако высокой точности ожидать здесь не следует. Согласно мнению ряда исследователей, включая С.П. Капицу, переход начался где-то между 65-м и 80-м годами прошлого века.

Начало демографического перехода С.П. Капица относит к моменту наивысшего набора скорости роста населения мира, а его конец — к моменту максимального спада прироста. Это не его определение, но оно полностью соответствует тому физикалистскому подходу к проблеме гиперболического роста населения планеты, которого он всегда придерживался. При таком определении столь глобальные события, как конец эпохи гиперболического роста и момент завершения перехода (полное прекращение роста), выступают как мгновенные, «точечные» характеристики процесса.

Что вряд ли может считаться удовлетворительным, поскольку при таком физикалистском подходе остается необъясненной парадоксальная устойчивость гиперболического роста, возвращающая рост всегда на одну и ту же, по сути, предзаданную гиперболу. Скорее всего, здесь мы имеем дело с нестационарным случайным процессом N(t), направленным во все времена на одну и ту же гиперболу демографического роста. Мгновенное значения скорости dN/dt в произвольный момент времени будет в таком случае всего лишь случайной величиной, и определять через нее такие глобальные характеристики системы «растущее человечество», как начало и конец перехода, — представляется неправильным.

Это неверное, по нашему мнению, определение и отодвинуло в прошлое дату начала перехода в расчетах С.П. Капицы примерно на 15 лет. Продолжительность демографического перехода в его модели составляет два характерных времени: 2τ = 42*2 = 84 года. Если отложить от момента начала перехода по Капице характерное время τ, получим ни о чем не говорящую, «безликую» дату 2007 год: 1965 + 42 = 2007 г. Дату, с которой не связано никакого глобального события истории, демографии и экономики и которая мало чем отличается от всех прочих дат первого десятилетия XXI века. (Мировой экономический кризис 2007–2012 гг. не был катастрофическим, и, кроме того, он никак не связан с демографическим переходом.) Но если сместить начало перехода на 15 лет в будущее, то момент окончания первого цикла перехода (1980 + 42 = 2022 г.) совпадет с сингулярностью гиперболы Форстера — сингулярностью Дьяконова-Капицы. Что еще раз указывает на ошибочность представления о том, что демографический переход начался в 1965 году.

Считая, что переход начался в конце семидесятых годов прошлого века и принимая для сингулярности гиперболы Форстера значение to = 2022—2032 г., получаем по самой грубой оценке для численности населения мира на момент начала перехода значение K5 ~ 4 млрд. человек и для времени до сингулярности τ ~ 50 лет. Если бы удалось каким-то образом найти одну из постоянных Капицы K или τ, вторую можно было бы определить, используя формулу закона гиперболического роста. Но какую из существующих аппроксимирующих зависимостей взять с учетом того, что теоретический закон нам не известен? Гиперболу Форстера, Хорнера или арккотангенсоиду Капицы, при уходе в прошлое переходящую в феноменологическую гиперболу Капицы?

Существует семейство гипербол, почти столь же хорошо отвечающих демографическим данным за последние двадцать столетий, как и гипербола Форстера, каждую из которых можно полностью задать с помощью тройки [C, p, to]. Как с помощью констант C, p, to построить гиперболу демографического роста? Каждая из этих констант определяет этап преобразования простейшей гиперболы N = -1/t. Сначала сдвигаем ее вдоль оси времени на to единиц вправо, затем переходим к более крутой (пологой) гиперболе N=1/(tо-t)^p, и, наконец, равномерно растягиваем ее в С раз вдоль оси N: N = С/(tо - t)^p.

Точность переменной численности населения Земли N(t), при ее определении по формуле Форстера, менее всего зависит от константы to, т.к. она вычислена Форстером с очень хорошей (в несколько лет) точностью. Следовательно, даже в первой половине ХХ века любая вариация to в пределах доверительного интервала практически не влияет на результат. Здесь еще нужно учесть то, что динамика изменения численности населения мира даже в ХХ-м веке известна с точностью до нескольких процентов, а также и то, что во второй половине ХХ века начался демографический переход, и формула Форстера перестала правильно описывать рост.

Из двух оставшихся констант [C, p] наиболее важной, в плане ее максимально точного определения, является показатель степенной зависимости р (степенная функция гораздо более чувствительна к относительному изменению ее показателя по сравнению с аналогичным изменением основания или мультипликативной константы), который характеризует степень, с которой гипербола «прижата» к осям времени и численности. Даже небольшая, в доли процента, его вариация может существенно повлиять на результат, причем во всем диапазоне исторического времени.

Изменение постоянной Форстера С определяет равномерное растяжение (сжатие) исходной гиперболы роста от/к оси времени, и поэтому точность в ее определении важна при подсчете численности во все времена. Точность, с которой могут быть определены постоянные Капицы K и τ, напрямую зависит от точности, с которой вычислена пара [C, p] в соответствии с условием С = K²∙τ^p.

Хотя действительный (теоретический) закон роста, как мы показали ранее, — это гипербола с целочисленным показателем p = 1, но если в результате обработки демографических данных по методу наименьших квадратов средняя аппроксимирующая гипербола получилась с дробным показателем, то при определении К и τ нужно исходить из обобщенного условия С = K₅∙τ^p = K²∙τ^p. Использовать для этой цели уравнение С = K²∙τ, как это делает С.П. Капица, представляется ошибочным.

Почему это так? Дело в том, что эмпирическая гипербола, заданная тройкой [C, p, to] меньше отличается (отстоит на меньшее расстояние) от теоретической гиперболы, соответствующей закону гиперболического роста [C', 1, to'] (где C' и to' неизвестны), чем гипербола, определяемая тройкой [C, 1, to], у которой p = 1, а С и to остаются теми же, что у эмпирической гиперболы или каким-то случайным образом варьируются.

Поэтому характерное время и характерная численность (сторонние, не связанные со степенным законом роста) для обобщенного закона, определяющего гиперболу [C, p, to], ближе к тем, что могли бы быть вычислены для закона гиперболического роста с целочисленным показателем p = 1, будь этот закон ([C', 1, to']) известен.
Например, если бы удалось каким-то образом оценить характерное время τ, то характерную численность K следовало бы вычислять в соответствии с условием С = K₅∙τ^p = K²∙τ^p, а не с С = K₅∙τ = K²τ.

Допустим, например, что характерное время τ связано с каким-то циклическим процессом, и длительность этого цикла известна с хорошей точностью. Или нет никакого такого цикла, а момент отхода роста от гиперболы найден с достаточно хорошей точностью, исходя из анализа общей его динамики во второй половине ХХ столетия.

В таком случае значение константы K₅ следует искать в соответствии с эмпирической зависимостью Форстера рис.8: N(to-τ) = K₅ = C/τ^p, где C = 179 млрд., n = -0.99, а не по формуле Капицы: N(to-τ) = K₅ = C/τ, где C = 163 (187?) млрд., n = -1. Поскольку эта зависимость позволяет с наибольшей точностью вычислить полное число живущих в каждый год от начала новой эры и до начала перехода.

Поэтому значение численности на момент начала перехода, вычисленное по эмпирической формуле Форстера, будет более точным, чем в соответствии с феноменологическим уравнением Капицы. Кроме того, об этом же говорит и теория размерностей. Нельзя определять характерную численность по формуле K₅ = К² = C/τ, как это делает С.П. Капица, поскольку постоянная Форстера, которую он использует в своих подсчетах, имеет размерность [год]^0.99.

Рис. 8. Теоретический и эмпирический законы роста численности населения Земли.

Так, если взять C = 186 млрд., К = 67000, как он полагал в своей первой статье 1992 года, то при р = 1 получаем τ = 41.4 года, а при р = 0.99, τ = 43.0 года. Если же взять С = 163 млрд. и К = 60100, как в его последней работе 2010 года [21], то при р = 1, τ = 45.2 года, а при р = 0.99, τ = 46.9 лет. Разница для характерного времени в обоих случаях слишком велика, чтобы пользоваться приближенной формулой С = K₅∙τ = K²τ, вместо точной С = K₅∙τ^p = K²∙τ^p. Неоднократно изменяя свои константы К и τ, С.П. Капица никогда не связывает каждую такую пару с показателем степенной функции "р" в феноменологической формуле Форстера. И это, на наш взгляд, может рассматриваться как серьезная ошибка.

В книге «Парадоксы роста» на стр. 170 читаем: «При обращении к последним данным демографии были получены уточненные значения постоянных: С = 63 млрд., и К = 60100, τ = 45 лет; K = (C/τ)^0.5". При этом подразумевается, что p = 1; на самом же деле значению С = 163 млрд. в семейство гипербол, аналогичных гиперболе Форстера, должен соответствовать некий неизвестный показатель р, значение которого при подсчете своих постоянных С.П. Капица никак не учитывает. Можно ли в таком случае доверять тем оценкам для τ и К, которые он получил?

Попробуем определить константы Капицы, исходя из нашей гипотезы. Поскольку характерная численность получена нами теоретически, и равна К = 2¹⁶ = 65536, остается только, исходя из формулы Форстера, определить характерное время τ. При р = 1, τ = 41.7 года, а при р = 0.99, τ = 43.3 года. Итак, если исходить из данных Форстера, получаем, что среднее значение характерного времени равно 43.3 года, а его действительное значение лежит в пределах: [41.8; 44.9] ≈ [42; 45] лет, что отличается от результатов С.П. Капицы. Так, в первой своей работе [1] он дает оценку τ = 41.4 года, а в последней [21], τ = 45.2 года. Обе эти оценки характерного времени лежат за пределами полученного нами доверительного интервала.

<<<назад содержание вперед>>>